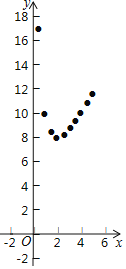题目内容
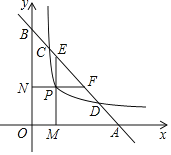
【题目】如图,直线y=﹣x+4分别交x轴、y轴于A、B两点,P是反比例函数y=![]() (x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(x>0),图象上位于直线y=﹣x+4下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,并且AFBE=4
(1)求k的值;
(2)若反比例函数y=![]() 与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
与一次函数y=﹣x+4交于C、D两点,求三角形OCD的面积.
【答案】(1)2;(2)4![]() .
.
【解析】
(1)由直线y=﹣x+4交x轴、y轴于A、B两点,即可得出∠OAB=∠OBA=45°,进而即可得出OM=BEsin∠OBA、ON=AFsin∠OAB,再结合AFBE=4即可得出OMON=2,此题得解;
(2)求出点C、D的坐标,然后连接OC、OD,根据S△OCD=S△AOB﹣S△AOD﹣S△BOC,根据三角形的面积公式列式计算即可得解;
解:(1)∵直线y=﹣x+4交x轴、y轴于A、B两点,
∴∠OAB=∠OBA=45°,
∴OM=BEsin∠OBA,ON=AFsin∠OAB.
∵AFBE=4,
∴OMON=![]() BE
BE![]() AF=2,
AF=2,
∴k=OMON=2.
(2)∵直线y=﹣x+4交x轴、y轴于A、B两点,
∴A(4,0),B(0,4),
解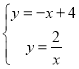 得
得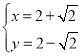 或
或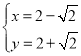 ,
,
∴C(2﹣![]() ,2+
,2+![]() ),D(2+
),D(2+![]() ,2﹣
,2﹣![]() ),
),
∴S△OCD=S△AOB﹣S△AOD﹣S△BOC,
=![]() ×4×4﹣
×4×4﹣![]() ×4×(2﹣
×4×(2﹣![]() )﹣
)﹣![]() ×4×(2﹣
×4×(2﹣![]() ),
),
=4![]() .
.

故答案为:(1)2;(2)4![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
【题目】小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整:
建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米.则y关于x的函数表达式为________;列表(相关数据保留一位小数):
根据函数的表达式,得到了x与y的几组值,如下表:
x | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y | 17 | 10 | 8.3 | 8.2 | 8.7 | 9.3 | 10.8 | 11.6 |
描点、画函数图象:
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
观察分析、得出结论:
根据以上信息可得,当x=________时,y有最小值.
由此,小强确定篱笆长至少为________米.