题目内容
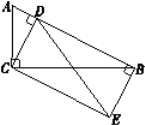
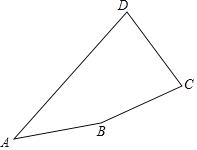
【题目】如图，在凸四边形ABCD中，AB＝BC＝CD，∠ABC+∠BCD＝240°．设∠ABC＝α．
（1）利用尺规，以CD为边在四边形内部作等边△CDE．（保留作图痕迹，不需要写作法）
（2）连接AE，判断四边形ABCE的形状，并说明理由．
（3）求证：∠ADC＝
α；
（4）若CD＝6，取CD的中点F，连结AF，当∠ABC等于多少度时，AF最大，最大值为多少．（直接写出答案，不需要说明理由）．
【答案】(1)见解析;(2)见解析;(3)见解析;(4)见解析.
【解析】
（1）①分别以C、D为圆心，以CD从为半径画弧，两弧交于点E，②连接DE、CE，△CDE即为所求；
（2）由等边三角形的性质得出∠CDE=∠CED=∠DCE=60°，DE=CE=CD，得出AB=CE，∠ABC+∠BCE=180°，证出AB∥CE，得出四边形ABCE是平行四边形，即可得出结论；
（3）连接AC，由菱形的性质得出AE=CE=DE，∠ABC=∠AEC，得出点E是△ACD的外接圆圆心，由圆周角定理得出∠AEC=2∠ADC，即可得出结论；
（4）当A、E、F三点共线时，AF的值最大=AE+EF，由等边三角形的性质和勾股定理求出EF=
DF=3，得出AF=AE+EF=6+3，求出∠ADC=75°，由（3）得：∠ABC=2∠ADC=150°即可．
（1）解：如图1所示：
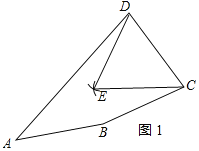
①分别以C、D为圆心，以CD从为半径画弧，两弧交于点E，
②连接DE、CE，
△CDE即为所求；
（2）如图2所示：
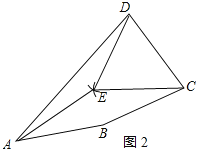
四边形ABCE是菱形；理由如下：
∵△CDE是等边三角形，
∴∠CDE＝∠CED＝∠DCE＝60°，DE＝CE＝CD，
∵AB＝BC＝CD，∠ABC+∠BCD＝240°，
∴AB＝CE，∠ABC+∠BCE＝240°﹣60°＝180°，
∴AB∥CE，
∴四边形ABCE是平行四边形，
∵AB＝BC，
∴四边形ABCE是菱形；
（3）证明：连接AC，如图3所示：
∵四边形ABCE是菱形，
∴AE＝CE＝DE，∠ABC＝∠AEC，
∴点E是△ACD的外接圆圆心，
∴∠AEC＝2∠ADC，
∴∠ABC＝2∠ADC，
∴∠ADC＝
α；
（4）如图4所示：
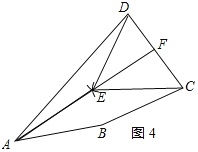
当A、E、F三点共线时，AF的值最大＝AE+EF，
∵△CDE是等边三角形，F是D的中点，
∴EF⊥CD，DF＝3，∠DEF＝∠CED＝30°，
∴EF＝DF＝3，
∴AF＝AE+EF＝6+3，
由（2）得：AE＝CE＝CD＝DE＝6，
∴∠EAD＝∠EDA＝∠DEF＝15°，
∴∠ADC＝15°+60°＝75°，
由（3）得：∠ABC＝2∠ADC＝150°，
∴当∠ABC等于150°时，AF最大，最大值为6+3．
