题目内容
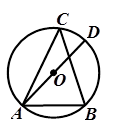
如图,已知AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠D=30°.
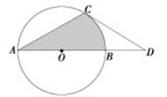
(1)求证:CA=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积S.

(1)求证:CA=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积S.
(1)见解析(2) +
+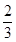
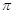
 +
+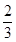
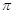
解:(1)证明:连结OC,∵过点C作⊙O的切线交AB的延长线于点D,∴OC⊥CD;
∵∠D=30°,∴∠DOC=60°;∵OA=OC,∴∠CAO=30°=∠D;∴CA=CD(4分)
(2)连结CB,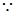 AB为⊙O的直径,∠CAO=30°,⊙O的半径为2∴CB=2,AC=2
AB为⊙O的直径,∠CAO=30°,⊙O的半径为2∴CB=2,AC=2
过点C作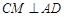 交于点M. ∴CM=
交于点M. ∴CM= ,
,
∴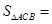
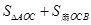 =
=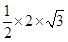 +
+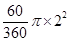 =
= +
+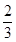
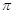 (4分)
(4分)
(1)连接OC,利用切线的性质和圆的半径相等即可证明CA=CD;
(2)过O作OE⊥AC于E,有图形可知,图中阴影部分的面积S=S△AOC+S扇形COB,分别求出三角形的面积和扇形的面积即可.
∵∠D=30°,∴∠DOC=60°;∵OA=OC,∴∠CAO=30°=∠D;∴CA=CD(4分)
(2)连结CB,
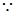 AB为⊙O的直径,∠CAO=30°,⊙O的半径为2∴CB=2,AC=2
AB为⊙O的直径,∠CAO=30°,⊙O的半径为2∴CB=2,AC=2
过点C作
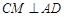 交于点M. ∴CM=
交于点M. ∴CM= ,
,∴
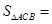
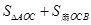 =
=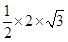 +
+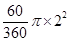 =
= +
+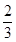
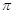 (4分)
(4分)(1)连接OC,利用切线的性质和圆的半径相等即可证明CA=CD;
(2)过O作OE⊥AC于E,有图形可知,图中阴影部分的面积S=S△AOC+S扇形COB,分别求出三角形的面积和扇形的面积即可.

练习册系列答案
相关题目
 的长为【 】
的长为【 】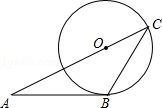
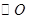 半径
半径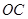 垂直于弦
垂直于弦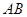 ,点
,点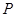 在
在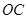 的延长线上,
的延长线上,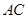 平分
平分 .
.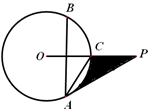
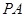 是
是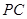 =
=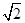 ,
,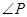 =30°,求阴影部分面积.(保留根号和
=30°,求阴影部分面积.(保留根号和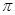 )
)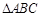 中,
中,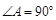 ,
, 是
是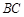 边上一点,以
边上一点,以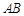 、
、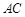 边相切于
边相切于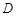 、
、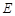 两点,连接
两点,连接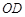 .已知
.已知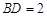 ,
,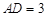 .求:
.求: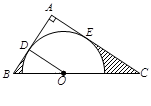
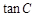 ;
;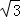 cm
cm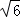 cm
cm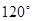 ,OC长为8cm,贴纸部分CA长为15cm,则贴纸部分面积为
,OC长为8cm,贴纸部分CA长为15cm,则贴纸部分面积为 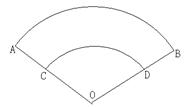
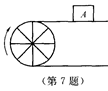
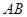 是湖上的一座桥,已知桥AB 长100m,测得圆周角
是湖上的一座桥,已知桥AB 长100m,测得圆周角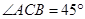 ,则这个人工湖的直径
,则这个人工湖的直径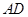 为
为