题目内容
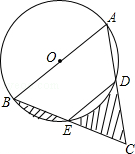
如图,在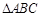 中,
中,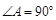 ,
, 是
是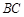 边上一点,以
边上一点,以 为圆心的半圆分别与
为圆心的半圆分别与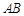 、
、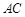 边相切于
边相切于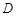 、
、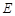 两点,连接
两点,连接 .已知
.已知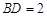 ,
,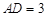 .求:
.求:
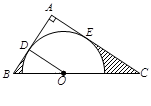
(1)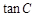 ;
;
(2)图中两部分阴影面积的和.
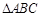 中,
中,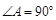 ,
, 是
是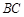 边上一点,以
边上一点,以 为圆心的半圆分别与
为圆心的半圆分别与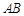 、
、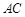 边相切于
边相切于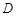 、
、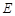 两点,连接
两点,连接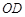 .已知
.已知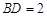 ,
,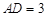 .求:
.求:
(1)
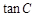 ;
;(2)图中两部分阴影面积的和.
(1)2/3,(2) 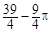
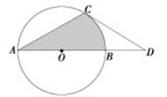
解:(1)连接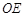
∵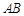 、
、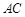 分别切
分别切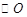 于
于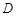 、
、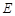 两点
两点
∴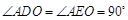
又∵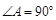
∴四边形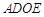 是矩形
是矩形
∵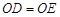
∴四边形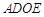 是正方形. .................................(2分)
是正方形. .................................(2分)
∴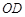 ∥
∥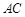 ,
,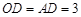
∴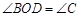
∴在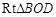 中,
中,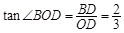
∴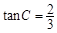 . .................................(5分)
. .................................(5分)
(2)如图,设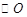 与
与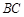 交于
交于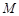 、
、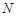 两点.由(1)得,四边形
两点.由(1)得,四边形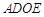 是正方形
是正方形

∴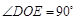
∴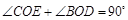
∵在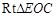 中,
中,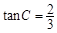 ,
,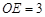
∴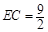 . .................................(7分)
. .................................(7分)
∴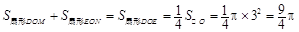
∴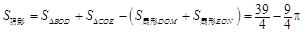
∴图中两部分阴影面积的和为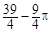 ............ 9分
............ 9分
(1)连接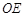 ,求得四边形
,求得四边形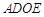 是正方形,得出AD的长,从而求得
是正方形,得出AD的长,从而求得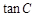
(2)根据阴影面积等于三角形的面积减去扇形的面积求得
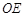
∵
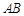 、
、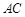 分别切
分别切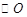 于
于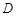 、
、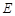 两点
两点∴
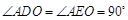
又∵
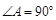
∴四边形
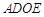 是矩形
是矩形 ∵
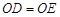
∴四边形
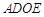 是正方形. .................................(2分)
是正方形. .................................(2分)∴
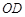 ∥
∥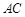 ,
,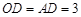
∴
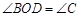
∴在
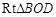 中,
中,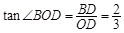
∴
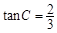 . .................................(5分)
. .................................(5分)(2)如图,设
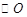 与
与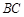 交于
交于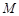 、
、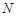 两点.由(1)得,四边形
两点.由(1)得,四边形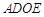 是正方形
是正方形
∴
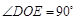
∴
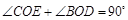
∵在
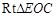 中,
中,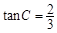 ,
,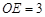
∴
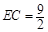 . .................................(7分)
. .................................(7分)∴
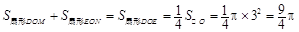
∴
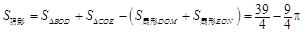
∴图中两部分阴影面积的和为
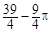 ............ 9分
............ 9分(1)连接
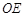 ,求得四边形
,求得四边形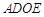 是正方形,得出AD的长,从而求得
是正方形,得出AD的长,从而求得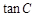
(2)根据阴影面积等于三角形的面积减去扇形的面积求得

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
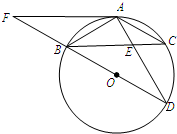
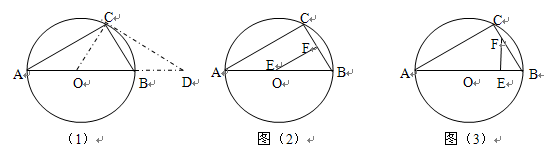
 ,连结EF,当
,连结EF,当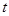 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.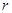 的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆, 那么这个内切圆的半径是 .
的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆, 那么这个内切圆的半径是 .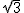 ,则顶点A运动到点A″的位置时,
,则顶点A运动到点A″的位置时,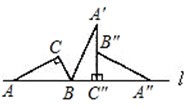
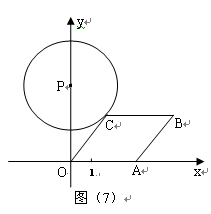
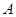 点从点(1,0)出发,以每秒1个单位长的速度沿着
点从点(1,0)出发,以每秒1个单位长的速度沿着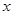 轴的正方向运动,经过
轴的正方向运动,经过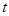 秒后,以
秒后,以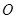 、
、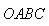 ,使
,使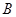 、
、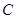 点都在第一象限内,且
点都在第一象限内,且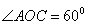 ,又以
,又以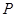 (0,4)为圆心,
(0,4)为圆心,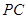 为半径的圆恰好与
为半径的圆恰好与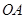 所在直线相切,则
所在直线相切,则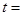 .
.