题目内容
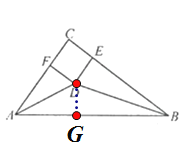
【题目】如图,在△ABC中,∠C=90°,∠A,∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.
⑴ 求证:四边形CFDE是正方形; ⑵ 若AC=3,BC=4,求△ABC的内切圆半径.

【答案】(1)见解析;(2)1.
【解析】
(1)过D作DG⊥AB交AB于G点,由角平分线性质得出DF=DG,同理可得DE=DG,则DE=DF,再由∠C=∠CFD=∠CED=90°可得四边形CFDE是正方形;
(2)先计算AB的长,由AF=AG,BE=BG得出AF+BE=AB,从而得到2CE=AC+CB-AB=2,求得CE=1,△ABC的内切圆半径为1.
过D作DG⊥AB交AB于G点,如图所示:
∵AD是∠BAC的角平分线,
∴DF=DG,同理可证DE=DG,
∴DE=DF,
∵∠C=∠CFD=∠CED=90°,
∴四边形CFDE是正方形;
⑵ ∵AC=3,BC=4,
∴AB=5,由⑴知AF=AG,BE=BG,
∴AF+BE=AB,
∵四边CFDE是正方形,
∴2CE=AC+CB-AB=2,即CE=1,△ABC的内切圆半径为1.

练习册系列答案
相关题目