题目内容
8.已知正数a,b有下列结论:①若ab=1,则a+b≥2,即a+b的最小值为2.
②若ab=4,则a+b≥4,即a+b的最小值为4.
③若ab=9,则a+b≥6,即a+b的最小值为6.
④若ab=16,即a+b≥8,即a+b的最小值为8.
根据以上所提供的规律猜想:
若a>0,b>0,且ab=100,求a+b的最小值.
分析 先找规律,得到通项公式,然后再运用公式解决问题
解答 解:因为①可变形为若ab=12时,a+b≥1×2,即a+b的最小值为2.
②可变形为若ab=22时,a+b≥2×2,即a+b的最小值为4.
③可变形为若ab=32时,a+b≥3×2,即a+b的最小值为6.
④可变形为若ab=42时,a+b≥4×2,即a+b的最小值为8.
根据以上所提供的规律猜想:若a>0,b>0,ab=n2时,a+b≥n×2,即a+b的最小值为2n,
所以若a>0,b>0,且ab=102,a+b≥10×2,求a+b的最小值为20.
点评 本题考查了完全平方公式的变形a+b≥2$\sqrt{ab}$,根据已知找出规律是解决问题的关键.

练习册系列答案
相关题目
20.已知x=5是方程x-4+a=3的解,则a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
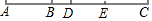 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.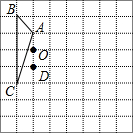 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)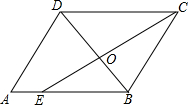 如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,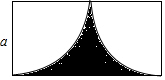 如图,长方形的宽为a,用式子表示阴影部分的面积,并计算当a=2时阴影部分的面积.(结果保留π)
如图,长方形的宽为a,用式子表示阴影部分的面积,并计算当a=2时阴影部分的面积.(结果保留π)