题目内容
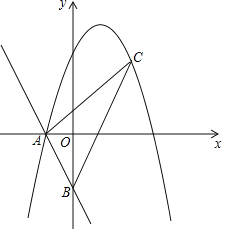
【题目】抛物线y＝﹣
x2+ax+b交x轴于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是抛物线在第一象限上的一点，过点P作AC的平行线l，分别交直线BC，y轴于点D，点E．
（1）填空：直线AC的解析式为 ，抛物线的解析式为 ；
（2）当CD＝
时，求OE的长；
（3）当DP＝DE时，求点P的横坐标．
【答案】（1）y＝2x+4，抛物线的解析式为
；（2）OE的长为1；（3）点P的横坐标1
【解析】
（1）先用待定系数法求出抛物线解析式，然后求出点、C坐标，再求直线AC的解析式即可；
（2）作BF//y轴，交DE于F．求出直线DE的解析式，表示出CE、BF的长，利用△CDE∽△BDF，列式求解即可；
（3）作PG//y轴，交BC于G．由△CED≌△GPD，可得PG=CE．求出直线BC的解析式，根据PG=CE列方程求解即可．
（1）把A(﹣2，0)，B(4，0)代入y＝﹣
x2+ax+b得，
，
解得
，
∴．
当x=0时，y=4，
∴C(0，4)，
设直线AC的解析式为y=mx+n，
，
，
∴y＝2x+4；
（2）如图，作BF//y轴，交DE于F．
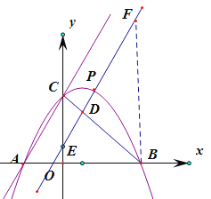
∵B(4，0)，C(0，4)，
∴BC=4
，
∵CD=，
∴BD=3．
设DE的解析式为y=2x+b，则E(0，b)，CE=4-b，
当x=4时，y=8+b，则BF=8+b，
∵BF//y轴，
∴△CDE∽△BDF，
∴
，
∴
，
解得
b=1，
∴OE=1；
（3）如图，作PG//y轴，交BC于G．
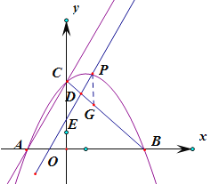
∵PG//y轴，
∴∠CED=∠GPD， ∠ECD=∠PGD，
∵DP＝DE，
∴△CED≌△GPD，
∴PG=CE．
设直线BC的解析式为y=ax+c，
∵B(4，0)，C(0，4)，
∴
，
解得
，
∴y=-x+4．
设P(m， 
)，G(m， )，
把P(m， )代入y=2x+b得
2m+b=，
∴b=
，
∴4-()=-()，
m2-m=0，
解得
m1=0（舍去），m2=1，
∴点P的横坐标1．
