题目内容
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
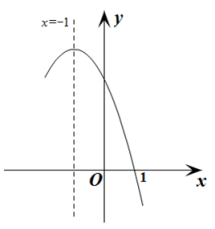
A.①③B.②④C.②③D.③④
【答案】D
【解析】
①根据抛物线开口方向、对称轴、与y轴的交点即可判断;
②根据抛物线的对称轴方程即可判断;
③根据抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1可得抛物线与x轴的另一个交点坐标为(﹣3,0),即可判断;
④根据m>n>0,得出m﹣1和n﹣1的大小及其与﹣1的关系,利用二次函数的性质即可判断.
解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①错误;
②∵对称轴为直线x=﹣1,
即﹣![]() =﹣1,解得b=2a,即2a﹣b=0,
=﹣1,解得b=2a,即2a﹣b=0,
所以②错误;
③∵抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
当a=﹣3时,y=0,即9a﹣3b+c=0,
所以③正确;
∵m>n>0,
∴m﹣1>n﹣1>﹣1,
由x>﹣1时,y随x的增大而减小知x=m﹣1时的函数值小于x=n﹣1时的函数值,故④正确;
故选:D.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
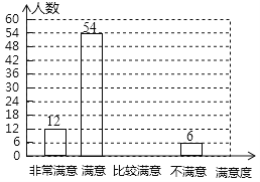
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.