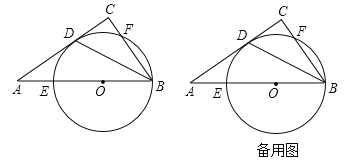
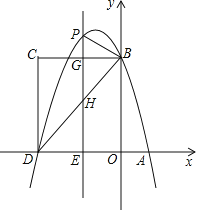
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻßy£½ax2+£Ø3b+1£©x+b©3£Øa£¾0£©£¬Čō“ęŌŚŹµŹżm£¬Ź¹µĆµćP£Øm£¬m£©ŌŚøĆÅ×ĪļĻßÉĻ£¬ĪŅĆĒ³ĘµćP£Øm£¬m£©ŹĒÕāøöÅ×ĪļĻßÉĻµÄŅ»øö”°ŗĶŠ³µć”±£®
£Ø1£©µ±a£½2£¬b£½1Ź±£¬ĒóøĆÅ×ĪļĻߵĔ°ŗĶŠ³µć”±£»
£Ø2£©Čō¶ŌÓŚČĪŅāŹµŹżb£¬Å×ĪļĻßÉĻŗćÓŠĮ½øö²»Ķ¬µÄ”°ŗĶŠ³µć”±A”¢B£®
¢ŁĒ󏵏żaµÄȔֵ·¶Ī§£»
¢ŚČōµćA£¬B¹ŲÓŚÖ±Ļßy£½©x©£Ø![]() +1£©¶Ō³Ę£¬Ē󏵏żbµÄ×īŠ”Öµ£®
+1£©¶Ō³Ę£¬Ē󏵏żbµÄ×īŠ”Öµ£®
”¾“š°ø”æ£Ø1£©£Ø![]() £©»ņ£Ø©2£¬©2£©£»£Ø2£©¢Ł0£¼a£¼27¢ŚbµÄ×īŠ”ÖµŹĒ
£©»ņ£Ø©2£¬©2£©£»£Ø2£©¢Ł0£¼a£¼27¢ŚbµÄ×īŠ”ÖµŹĒ![]()
”¾½āĪö”æ
£Ø1£©°Ńx=y=m£¬a=2£¬b=1“śČėŗÆŹż½āĪöŹ½£¬ĮŠ³ö·½³Ģ£¬Ķعż½ā·½³ĢĒóµĆmµÄÖµ¼“æÉ£»
£Ø2£©Å×ĪļĻßÉĻŗćÓŠĮ½øö²»Ķ¬µÄ”°ŗĶŠ³µć”±A”¢B£®Ōņ¹ŲÓŚmµÄ·½³Ģm=am2+£Ø3b+1£©m+b-3µÄøłµÄÅŠ±šŹ½”÷=9b2-4ab+12a£®
¢ŁĮīy=9b2-4ab+12a£¬¶ŌÓŚČĪŅāŹµŹżb£¬¾łÓŠy£¾0£¬ĖłŅŌøł¾Ż¶ž“ĪŗÆŹży=9b2-4ab+12µÄĶ¼ĻóŠŌÖŹ½ā“š£»
¢ŚĄūÓƶž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘŠŌÖŹ½ā“š¼“æÉ£®
£Ø1£©µ±a£½2£¬b£½1Ź±£¬m£½2m2+4m+1©4£¬
½āµĆm£½![]() »ņm£½©2£®
»ņm£½©2£®
ĖłŅŌµćPµÄ×ų±źŹĒ£Ø![]() £¬
£¬![]() £©»ņ£Ø©2£¬©2£©£»
£©»ņ£Ø©2£¬©2£©£»
£Ø2£©m£½am2+£Ø3b+1£©m+b©3£¬
”÷£½9b2©4ab+12a£®
¢ŁĮīy£½9b2©4ab+12a£¬¶ŌÓŚČĪŅāŹµŹżb£¬¾łÓŠy£¾0£¬Ņ²¾ĶŹĒĖµÅ×ĪļĻßy£½9b2©4ab+12µÄĶ¼Ļó¶¼ŌŚbÖį£ØŗįÖį£©ÉĻ·½£®
”ą”÷£½£Ø©4a£©2©4”Į9”Į12a£¼0£®
”ą0£¼a£¼27£®
¢ŚÓÉ”°ŗĶŠ³µć”±¶ØŅåæÉÉčA£Øx1£¬y1£©£¬B£Øx2£¬y2£©£¬
Ōņx1£¬x2ŹĒax2+£Ø3b+1£©x+b©3£½0µÄĮ½²»µČŹµøł£¬![]() £®
£®
”ąĻ߶ĪABµÄÖŠµć×ų±źŹĒ£ŗ£Ø©![]() £¬©
£¬©![]() £©£®“śČė¶Ō³ĘÖįy£½x©£Ø
£©£®“śČė¶Ō³ĘÖįy£½x©£Ø![]() +1£©£¬µĆ
+1£©£¬µĆ
©![]() £½
£½![]() ©£Ø
©£Ø![]() +1£©£¬
+1£©£¬
”ą3b+1£½![]() +a£®
+a£®
”ßa£¾0£¬![]() £¾0£¬a
£¾0£¬a![]() £½1ĪŖ¶ØÖµ£¬
£½1ĪŖ¶ØÖµ£¬
”ą3b+1£½![]() +a”Ż2
+a”Ż2![]() £½2£¬
£½2£¬
”ąb”Ż![]() £®
£®
”ąbµÄ×īŠ”ÖµŹĒ![]() £®
£®

 Ģį·Ö°Ł·Ö°Ł¼ģ²ā¾ķĻµĮŠ“š°ø
Ģį·Ö°Ł·Ö°Ł¼ģ²ā¾ķĻµĮŠ“š°ø ±¦±“¼Ę»®ĘŚÄ©³å“Ģ¶į100·ÖĻµĮŠ“š°ø
±¦±“¼Ę»®ĘŚÄ©³å“Ģ¶į100·ÖĻµĮŠ“š°ø ÄÜæ¼ŹŌČ«ÄÜ100·ÖĻµĮŠ“š°ø
ÄÜæ¼ŹŌČ«ÄÜ100·ÖĻµĮŠ“š°ø