题目内容
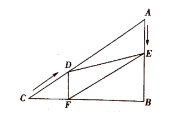
【题目】如图,矩形![]() 中,
中,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,则
,则![]() =_________.
=_________.
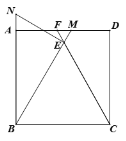
【答案】![]()
【解析】
通过四边形ABCD是矩形以及![]() ,得到△FEM是等边三角形,根据含30°直角三角形的性质以及勾股定理得到KM,NK,KE的值,进而得到NE的值,再利用30°直角三角形的性质及勾股定理得到BN,BE即可.
,得到△FEM是等边三角形,根据含30°直角三角形的性质以及勾股定理得到KM,NK,KE的值,进而得到NE的值,再利用30°直角三角形的性质及勾股定理得到BN,BE即可.
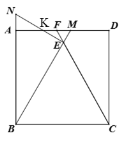
解:如图,设NE交AD于点K,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∴∠MFE=∠FCB,∠FME=∠EBC
∵![]() ,
,
∴△BCE为等边三角形,
∴∠BEC=∠ECB=∠EBC=60°,
∵∠FEM=∠BEC,
∴∠FEM=∠MFE=∠FME=60°,
∴△FEM是等边三角形,FM=FE=EM=2,
∵EN⊥BE,
∴∠NEM=∠NEB=90°,
∴∠NKA=∠MKE=30°,
∴KM=2EM=4,NK=2AN=6,
∴在Rt△KME中,KE=![]() ,
,
∴NE=NK+KE=6+![]() ,
,
∵∠ABC=90°,
∴∠ABE=30°,
∴BN=2NE=12+![]() ,
,
∴BE=![]() ,
,
∴BC=BE=![]() ,
,
故答案为:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目