题目内容
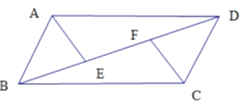
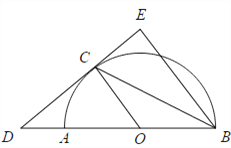
【题目】小明同学对平面图形进行了自主探究；图形的顶点数A，被分成的区域数B，线段数C三者之间是否存在确定的数量关系．如图是他在探究时画出的5个图形．
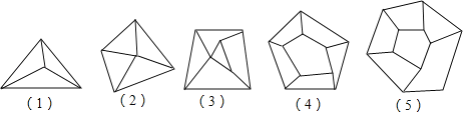
（1）根据图完成表格：
A | B | C | |
平面图形（1） |
| 3 | 6 |
平面图形（2） | 5 |
| 8 |
平面图形（4） | 10 | 6 |
|
（2）猜想：一个平面图形中顶点数A，区域数B，线段数C之间的数量关系是 ；
（3）计算：已知一个平面图形有24条线段，被分成9个区域，则这个平面图形的顶点有 个．
【答案】（1）4、4、15；（2）A+B﹣C＝1；（3）16．
【解析】
（1）观察图形可填表即可；
（2）先根据题（1）得到的表格数据，可得出平面图形（1）、（2）、（4）中满足的关系式，再归纳类推出一般规律；
（3）根据（2）中所得关系即可求解
（1）观察图形可知：
平面图形（1）中顶点数A为4
平面图形（2）中区域数B为4
平面图形（3）中线段数C为15
故答案为4、4、15；
（2）由题（1）得到的结果，观察表格数据可知：
平面图形（1）中顶点数、区域数、线段数满足：
平面图形（2）中顶点数、区域数、线段数满足：
平面图形（3）中顶点数、区域数、线段数满足：
猜想：一个平面图形中顶点数A，区域数B，线段数C之间的数量关系为
故答案为：；
（3）已知一个平面图形有24条线段，被分成9个区域，
即
，代入中
解得：
则这个平面图形的顶点有16个
故答案为16．
练习册系列答案
相关题目
