题目内容
【题目】根据下面给出的数轴,解答下面的问题:

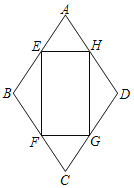
(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数A: B: ;
(2)观察数轴,与点A的距离为![]() 的点表示的数是: ;
的点表示的数是: ;
(3)若将数轴折叠,使得![]() 点与0表示的点重合,则B点与数 表示的点重合;
点与0表示的点重合,则B点与数 表示的点重合;
(4)若数轴上M、N两点之间的距离为2019(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则![]() 、
、![]() 两点表示的数分别是:M: ,N: .
两点表示的数分别是:M: ,N: .
【答案】(1)2,-1.5 ;(2)6或-2 ;(3)3.5;(4)-1008.5,1010.5
【解析】
(1)根据数轴写出即可;
(2)分点在A的左边和右边两种情况解答;
(3)设点B对应的数是x,然后根据对折点列式计算即可得解;
(4)根据M、N两点经过折叠后互相重合求出MN的一半,然后求出对折点,再分别列式计算即可得解.
解:(1)由数轴可得,A:2,B:1.5,
故答案为:2,-1.5;
(2)该点在A的左边时,表示的数为24=2,
该点在A的右边时,表示的数为2+4=6,
故答案为:2或6;
(3)设点B对应的数是x,
则![]() ,
,
解得x=3.5,
故答案为:3.5;
(4)∵M、N两点之间的距离为2019,
∴![]() ,
,
由(3)可知对折点为:![]() ,
,
∴点M为11009.5=1008.5,点N为1+1009.5=1010.5,
故答案为:-1008.5,1010.5.

【题目】小明同学对平面图形进行了自主探究;图形的顶点数A,被分成的区域数B,线段数C三者之间是否存在确定的数量关系.如图是他在探究时画出的5个图形.
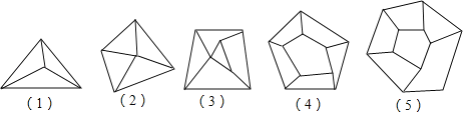
(1)根据图完成表格:
A | B | C | |
平面图形(1) |
| 3 | 6 |
平面图形(2) | 5 |
| 8 |
平面图形(4) | 10 | 6 |
|
(2)猜想:一个平面图形中顶点数A,区域数B,线段数C之间的数量关系是 ;
(3)计算:已知一个平面图形有24条线段,被分成9个区域,则这个平面图形的顶点有 个.