题目内容
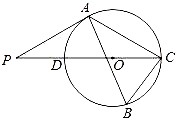
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若⊙O的半径为3,求阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OA,如图,先根据圆周角定理得到∠AOC=2∠B=120°,则∠AOP=60°,再计算出∠OCA的度数,接着利用AP=AC得到∠P=∠ACO=30°,然后根据三角形的内角和可计算出发∠APO=90°,于是利用切线的判定定理可判断出PA是⊙O的切线;
(2)在Rt△AOP中,利用含30度的直角三角形三边的关系得到PO=2OA=6,PA=![]() OA=3
OA=3![]() ,然后根据三角形面积公式和扇形面积公式进行计算即可.
,然后根据三角形面积公式和扇形面积公式进行计算即可.
试题解析:(1)连接OA,如图,

∵∠AOC=2∠B=120°,
∴∠AOP=60°,
∵OA=OC,
∴∠OCA=∠OAC=![]() (180°-120°)=30°,
(180°-120°)=30°,
∵AP=AC,
∴∠P=∠ACO=30°,
∴∠PAO=180°-30°-60°=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)在Rt△AOP中,PO=2OA=6,PA=![]() OA=3
OA=3![]() ,
,
∴S阴影部分=S△PAO-S扇形OAD=![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目