题目内容
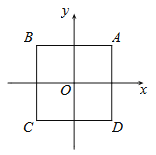
【题目】如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
(1)若函数y=x2+m的图象过点C,求这个函数的解析式;并判断其函数图象是否过A点.
(2)若将(1)中的函数图象先向右平移1个单位,再向上平移2个单位,直接写出平移后函数的解析式和顶点坐标.
【答案】(1)y=x2﹣2,其函数图象不过A点;(2)平移后的抛物线的顶点坐标为(1,0).
【解析】试题分析:(1)根据题意A(1,1),C(-1,-1),代入y=x2+m根据待定系数法即可求得解析式,把A的坐标代入即可判断;
(2)直接利用抛物线平移规律:上加下减,左加右减进而得出平移后的解析式,即可得出顶点坐标.
试题解析:
(1),由题意得A(1,1),C(﹣1,﹣1),
∵函数y=x2+m的图象过点C,
∴﹣1=1+m,
解得m=﹣2,
∴此函数的解析式为y=x2﹣2,
把A(1,1)代入y=x2﹣2的左右两边,
左边=1,右边=﹣1,左≠右,
∴其函数图象不过A点.
(2)∵将抛物线y=x2﹣2向上平移2个单位再向右平移1个单位,
∴平移后的抛物线的解析式为:y=(x﹣1)2﹣2+2.
即y=(x﹣1)2,
则平移后的抛物线的顶点坐标为:(1,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目