Question

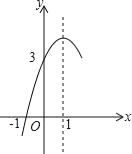
【题目】在平面直角坐标系xOy中，已知抛物线(k为常数）．

（1）若抛物线经过点(1,k2)，求k的值；

（2）若抛物线经过点(2k,y1)和点(2,y2)，且y1>y2，求k的取值范围；

（3）若将抛物线向右平移1个单位长度得到新抛物线，当1≤x≤2时，新抛物线对应的函数有最小值，求k的值．

Answer 1

【答案】(1);(2)k>1；（3）1或3.

【解析】

（1）把（1，k2）代入抛物线解析式中并求解即可；

（2）将点分别代入抛物线解析式中，由y1＞y2列出关于k的不等式，求解即可；

（3）先求出新抛物线的解析式，然后分1≤k≤2，k＞2以及k＜1三种情况讨论，根据二次函数的顶点及增减性，分别确定三种情况下各自对应的最小值，然后列出方程并求出满足题意的k值即可．

解：（1）把点代入抛物线，得

解得

（2）把点代入抛物线，得

把点代入抛物线，得

解得

（3）抛物线解析式配方得

将抛物线向右平移1个单位长度得到新解析式为

当时，对应的抛物线部分位于对称轴右侧，随的增大而增大，

时，，

，解得，

都不合题意，舍去；

当时，，

解得；

当时，对应的抛物线部分位于对称轴左侧，随的增大而减小，

时，，

解得，（舍去）

综上，或3．