Question

【题目】如图，在Rt△ABC中，∠C=90°，AC=8m，BC=6m，点P由C点出发以2m/s的速度向终点A匀速移动，同时点Q由点B出发以1m/s的速度向终点C匀速移动，当一个点到达终点时另一个点也随之停止移动．

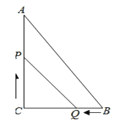
（1）经过几秒△PCQ的面积为△ACB的面积的？

（2）经过几秒，△PCQ与△ACB相似？

Answer 1

【答案】（1）2秒或4秒；（2）秒或秒

【解析】

（1）分别表示出线段PC和线段CQ的长后利用S△PCQ=S△ABC列出方程求解；
（2）设运动时间为ts，△PCQ与△ACB相似，当△PCQ与△ACB相似时，则有或，分别代入可得到关于t的方程，可求得t的值.

解：（1）设经过x秒△PCQ的面积为△ACB的面积的，

由题意得：PC=2xm，CQ=（6﹣x）m，

则×2x（6﹣x）=××8×6，

解得：x=2或x=4．

故经过2秒或4秒，△PCQ的面积为△ACB的面积的；

（2）设运动时间为ts，△PCQ与△ACB相似．

当△PCQ与△ACB相似时，则有或，

所以 ，或，

解得t=，或t=．

因此，经过秒或秒，△OCQ与△ACB相似；