题目内容
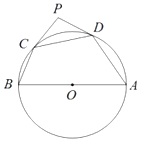
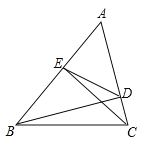
【题目】如图，在△ABC中，BD⊥AC于D，CE⊥AB于E。
（1）求证：△ABD∽△ACE
（2）连接DE，求证：∠ADE＝∠ABC
【答案】（1）见解析（2）见解析
【解析】
（1）由垂直的性质可得：∠ADB=∠AEC=90°，又因为∠BAD=∠CAE，所以△ABD∽△ACE；
（2）由（1）可知△ABD∽△ACE，所以
，又因为∠BAD=∠CAE，所以△ADE∽△ACB，由相似三角形的性质：对应角相等，即可得到∠ADE=∠ABC．
解：∵BD⊥AC于D，CE⊥AB于E.
∴∠ADB=∠AEC=90，
∵∠BAD=∠CAE，
∴△ABD∽△ACE；
(2)证明：
∵△ABD∽△ACE，
∴ADAE=ABAC，
∵∠BAD=∠CAE，
∴△ADE∽△ACB，
∴∠ADE=∠ABC.
练习册系列答案
相关题目
【题目】二次函数
（
是常数，
）的自变量
与函数值
的部分对应值如下表：
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当
时，与其对应的函数值
．有下列结论：①
；②
和3是关于的方程
的两个根；③
．其中，正确结论的个数是（ ）
A. 0B. 1C. 2D. 3
