题目内容
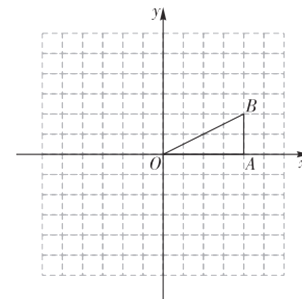
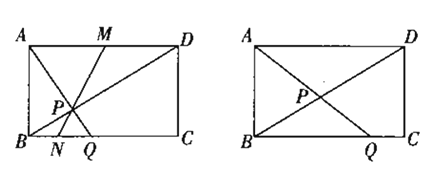
【题目】如图,矩形ABCD中,AB=a,AD=b,点P是对角线BD上的一个动点(点P不与B、D重合),连接AP并延长交射线BC于点Q,
(1)当AP⊥BD时,求△ABQ的面积(用含a、b的代数式表示).
(2)若点M为AD边的中点,连接MP交BC于点N,证明:点N也为线段BQ的中点.
(3)如图,当![]() 为何值时,△ADP与△BPQ的面积之和最小.
为何值时,△ADP与△BPQ的面积之和最小.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)由矩形性质,得到∠BAD=∠ABC=90°,由AP⊥BD,即可得到∠BAQ=∠ADB,则△ABQ∽△DAB,可得![]() ,可求出BQ,然后求出面积;
,可求出BQ,然后求出面积;
(2)由AD∥BC,得到△AMP∽△QNP,△DMP∽△BNP,然后得到![]() ,由AM=DM,即可得到NQ=BN;
,由AM=DM,即可得到NQ=BN;
(3)过点P作EF⊥AD交 AD、BC于 E 、F,设PE=h,则PF=a-h,根据对应线段成比例,求出BQ的值;然后根据面积之和,得到关于h的一元二次方程,利用根的判别式,求出面积的取值范围,当面积最小时,求出h的值,然后得到![]() 的值.
的值.
(1)解:如图:
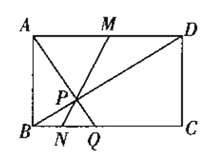
∵四边形ABCD是矩形,
∴AB=CD=a,BC=AD=b,∠BAD=∠ABC=90°,
∵AP⊥BD,
∴∠BAQ+∠QAD=90°, ∠QAD+∠ADB=90°,
∴∠BAQ =∠ADB,
∴△ABQ∽△DAB,
∴![]() ,
,
∴![]() ,
,
∴S△ABQ=![]() ;
;
(2) ∵四边形ABCD是矩形,
∴AD∥BC,
∴△AMP∽△QNP,△DMP∽△BNP,
∴![]() ,
,
∴![]() ,
,
∵点M是AD的中点,
∴AM=DM,
∴NQ=BN,
即点N是BQ的中点;
(3)如图,过点P作EF⊥AD交 AD、BC于 E 、F,
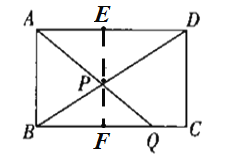
设PE=h,则PF=a-h,
∵AD∥BC,
∴![]() ,
,
∵AD=b,
∴BQ=![]() .
.
设△ADP和△BPQ的面积之和为S,则
![]()
=![]()
=![]()
=![]() ,
,
∴![]() ,
,
即:![]() ;
;
∵关于h的方程![]() ,有实数根,
,有实数根,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴S的最小值为:![]() ,
,
当![]() 时,代入方程
时,代入方程![]() ,
,
解得:![]() ;
;
∵AD∥BC,
∴![]() ,
,
∴当![]() 时,△ADP和△BPQ的面积之和最小.
时,△ADP和△BPQ的面积之和最小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小明和小李准备七月初到重庆或长沙去旅游,为了了解这两个城市哪个更热,他们查阅资料,收集了两个城市2018年七月前两周最高温度的记录,如下表:
日期(七月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
重庆最高温度/℃ | 33 | 36 | 34 | 31 | 31 | 30 | 30 | 33 | 34 | 36 | 37 | 35 | 37 | 37 |
长沙最高温度/℃ | 29 | 34 | 35 | 35 | 36 | 29 | 31 | 31 | 34 | 35 | 35 | 31 | 35 | 35 |
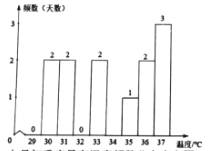
根据上表,他们将两个城市的最高温度分别绘制了如下的频数分布直方图和统计表,并对数据进行了整理
七月初重庆最高温度频数分布直方图
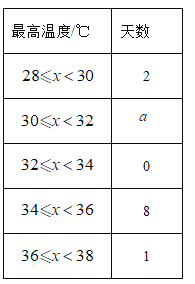
七月初长沙最高温度统计表
平均数/℃ | 中位数/℃ | 众数/℃ | 34/℃以上天数 | 30/℃以下天数 | |
重庆 | 33.9 | 34 | c | 6 | 0 |
长沙 | 33.2 | b | 35 | 7 | 2 |
请回答如下问题:
(1)本次调查的目的是________;
(2)补全频数分布直方图,并写出表中a,b,c的值,![]() ________,
________,![]() _____,c=___.
_____,c=___.
(3)结合以上分析,你认为七月初哪个城市更热,请写出两条支持你观点的理由.