题目内容
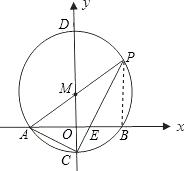
如图,在平面直角坐标系中,以点M(0,
)为圆心,以2
长为半径作⊙M交x轴 于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.
| 3 |
| 3 |
 于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.
(1)连接PB,
∵PA是⊙M的直径,
∴∠PBA=90度,
∵DC是⊙M的直径,且垂直于弦AB,
∴DC平分弦AB,
在Rt△AMO中AM=2
,OM=
,
∴AO=OB=3,
又∵MO⊥AB,
∴PB∥MO,
∴PB=2OM=2
,
∴P点坐标为(3,2
),
∵CM=2
,OM=
,
∴OC=CM-OM=
,
∴C(0,-
),直线CP过C,P两点,
设直线CP的解析式为y=kx+b(k≠0),
得到
,
解得:
,
∴直线CP的解析式为y=
x-
;
(2)在Rt△AMO中,∠AMO=60度,
又∵AM=CM,
∴△AMC为等边三角形,
∴AC=AM=2
,∠MAC=60度.
又∵AP为⊙M的直径,
∴∠ACP=90°,∠APC=30度,
PC=
AC=
•2
=6,
∴△ACP的面积=
AC•PC=
×2
×6=6
.
∵PA是⊙M的直径,
∴∠PBA=90度,
∵DC是⊙M的直径,且垂直于弦AB,
∴DC平分弦AB,
在Rt△AMO中AM=2
| 3 |
| 3 |
∴AO=OB=3,
又∵MO⊥AB,
∴PB∥MO,
∴PB=2OM=2
| 3 |
∴P点坐标为(3,2
| 3 |
∵CM=2
| 3 |
| 3 |
∴OC=CM-OM=
| 3 |
∴C(0,-
| 3 |
设直线CP的解析式为y=kx+b(k≠0),
得到
|
解得:
|
∴直线CP的解析式为y=
| 3 |
| 3 |
(2)在Rt△AMO中,∠AMO=60度,
又∵AM=CM,
∴△AMC为等边三角形,
∴AC=AM=2
| 3 |
又∵AP为⊙M的直径,
∴∠ACP=90°,∠APC=30度,
PC=
| 3 |
| 3 |
| 3 |
∴△ACP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |


练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

 点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).
点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).