题目内容
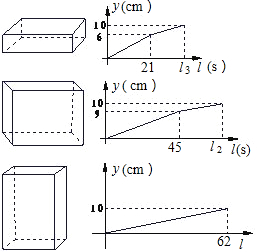
将长、宽、高分别为a，b，c（a＞b＞c，单位：cm）的三块相同的长方体按图所示的三种方式放入三个底面面直径为d（d＞
），高为h的相同圆柱形水桶中，再向三个水桶内以相同的速度匀速注水，直至注满水桶为止，水桶内的水深y（cm）与注水时间t（s）的函数关系如图所示，则注水速度为（ ）
| a2+b2 |
| A．30cm2/s | B．32cm2/s | C．34cm2/s | D．40cm2/s |
设水桶底面积为s，注水速度为v，
当水面刚刚过第二种放置的立方体上表面时，把立方体如图1放置，此时水面高于第一水面9-6=3（cm），时间差为45-21=24（s），于是得s×3=24×v，
由第三种放置得s×10-6×9×10=62×v，
解得v=30（cm2/s）．
故选A．
当水面刚刚过第二种放置的立方体上表面时，把立方体如图1放置，此时水面高于第一水面9-6=3（cm），时间差为45-21=24（s），于是得s×3=24×v，
由第三种放置得s×10-6×9×10=62×v，
解得v=30（cm2/s）．
故选A．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
于A，B两点，交y轴于C，D两点，连接AM并延长交⊙M于P点，连接PC交x轴于E．
