题目内容
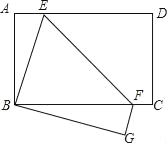
【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
【答案】![]()
【解析】如图所示:
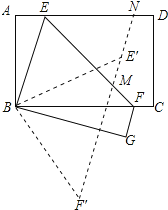
由折叠性质得:设AE=x=FC=FG,
则BE=ED=8-x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
即62+x2=(8-x)2,
解得:x=![]() ,
,
∴BE=8-![]() =
=![]() ,
,
EF=![]() =
=![]() ,
,
由折叠性质得:∠BEF=∠DEF=∠BFE,
∵EN=NM,
∴∠DEF=∠NME=∠F′,
∴EM∥BF′,BE∥E′F′,
∴四边形BEMF′为平行四边形,
由旋转性质得:BF′=BF=8-x,
∴BE=BF′,
∴平行四边形BEMF′为菱形,
∴EM=BE=![]() ,
,
∴FM=EF-EM=![]() .
.
故答案是:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在一次交通调查中,100辆汽车经过某地时车内人数如下:
乘车人数 | 1 | 2 | 3 | 4 | 5 |
车数 | x | 30 | y | 16 | 4 |
(1)x+y= .
(2)若每辆车的平均人数为2.5,则中位数为 人.
(3)若每辆车的平均人数为2,则众数为 人.
(4)若x为30,则每辆车的平均人数为 人,中位数为 人.
