��Ŀ����
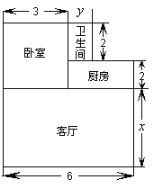
����Ŀ����һ�߳�Ϊ40cm��������Ӳֽ�壬�����ʵ��ļ��ã��۳�һ�������κ��ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ��� 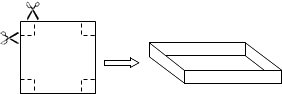
��1����ͼ������������Ӳֽ����ĽǸ���һ��ͬ����С�������Σ���ʣ�ಿ���۳�һ���ǵij����κ��ӣ� ��Ҫʹ�۳ɵij����κ��ӵĵ����Ϊ484cm2 �� ��ô�����������εı߳�Ϊ���٣�
���۳ɵij����κ��ӵIJ�����Ƿ������ֵ������У����������ֵ�ʹ�ʱ�����������εı߳������û�У�˵�����ɣ�
��2������������Ӳֽ������ܼ���һЩ���Σ��������ľ���������һ������������Ӳֽ��ı��ϣ�����ʣ�ಿ���۳�һ���иǵij����κ��ӣ����۳ɵ�һ�������κ��ӵı����Ϊ550cm2 �� ���ʱ�����κ��ӵij��������ߣ�ֻ���������Ҫ���һ���������
���𰸡�
��1���⣺��������������εı߳�Ϊxcm��
��40��2x��2=484��
��40��2x=��22��
���x1=31���������⣬��ȥ����x2=9��
������������εı߳�Ϊ9cm��
�ڲ���������ֵ��
�������С�����εı߳�Ϊacm�����ӵIJ����Ϊycm2��
��y��a�ĺ�����ϵΪ��y=4��40��2a��a��
��y=��8a2+160a��
��y=��8��a��10��2+800��
��a=10ʱ��y���=800��
���������������εı߳�Ϊ10cmʱ�������κ��ӵIJ�������Ϊ800cm2
��2���⣺����ͼ��һ�ּ���ͼ�У�������ij����κ��ӵı߳�Ϊxcm��
2��40��2x����20��x��+2x��20��x��+2x��40��2x��=550��
��ã�x1=��35���������⣬��ȥ����x2=15��
������ij����κ��ӵı߳�Ϊ15cm��
40��2��15=10��cm����
20��15=5��cm����
��ʱ��������ӵij�Ϊ15cm����Ϊ10cm����Ϊ5cm��
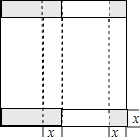
����������1���ټ�������������εı߳�Ϊxcm����������ó���40��2x��2=484��������ɣ��ڼ�������������εı߳�Ϊacm�����ӵIJ����Ϊycm2 �� ��y��x�ĺ�����ϵΪ��y=4��40��2a��a�����ö��κ�����ֵ������ɣ���2����������ij����κ��ӵĸ�Ϊtcm�������۳ɵ�һ�������κ��ӵı����Ϊ550cm2 �� �ó���ʽ����������ɣ�

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�����Ŀ��һ����Ͷ�����Թ涨����6������Ϊ�ϸ�9������Ϊ���㣬�ס�������ͬѧ��һ�β��Գɼ����£�
�ɼ����֣� | 4 | 5 | 6 | 7 | 8 | 9 |
���飨�ˣ� | 1 | 2 | 5 | 2 | 1 | 4 |
���飨�ˣ� | 1 | 1 | 4 | 5 | 2 | 2 |
��1�������������ͳ�����ݣ��������ͼ�ͱ����������� 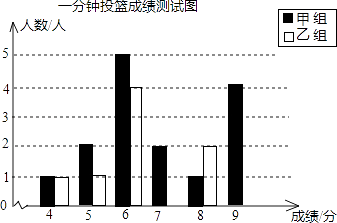
һ����Ͷ���ɼ�ͳ�Ʒ�������
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� | 2.56 | 6 | 80.0% | 26.7% | |
���� | 6.8 | 1.76 | 86.7% | 13.3% |
��2��������С����С�ϵ�һ�ζԻ���������ݣ�1���еı���д������֧��С�ϵĹ۵�����ɣ�