题目内容
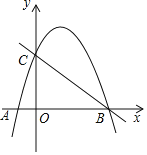
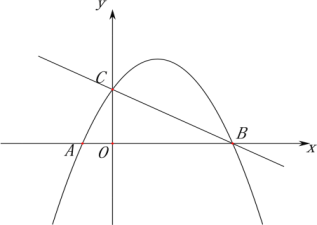
【题目】如图,矩形![]() 摆放在平面直角坐标系
摆放在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)求直线![]() 的表达式;
的表达式;
(2)若直线![]() 与矩形
与矩形![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与矩形
与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由条件可求得A、C的坐标,利用待定系数法可求得直线AC的表达式;
(2)结合图形,当直线平移到过C、A时与矩形有一个公共点,则可求得b的取值范围;
(3)由题意可知直线l过(0,10),结合图象可知当直线过B点时与矩形有一个公共点,结合图象可求得k的取值范围.
解:
(1) ![]()
![]() ,
,
设直线![]() 表达式为
表达式为![]() ,
,
![]() ,解得
,解得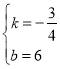
![]() 直线
直线![]() 表达式为
表达式为![]() ;
;
(2) ![]() 直线
直线![]() 可以看到是由直线
可以看到是由直线![]() 平移得到,
平移得到,
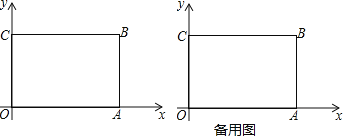
![]() 当直线
当直线![]() 过
过![]() 时,直线与矩形
时,直线与矩形![]() 有一个公共点,如图1,
有一个公共点,如图1,

当过点![]() 时,代入可得
时,代入可得![]() ,解得
,解得![]() .
.
当过点![]() 时,可得
时,可得![]()
![]() 直线
直线![]() 与矩形
与矩形![]() 有公共点时,
有公共点时,![]() 的取值范围为
的取值范围为![]() ;
;
(3) ![]() ,
,
![]() 直线
直线![]() 过
过![]() ,且
,且![]() ,
,
如图2,直线![]() 绕点
绕点![]() 旋转,当直线过点
旋转,当直线过点![]() 时,与矩形
时,与矩形![]() 有一个公共点,逆时针旋转到与
有一个公共点,逆时针旋转到与![]() 轴重合时与矩形
轴重合时与矩形![]() 有公共点,
有公共点,
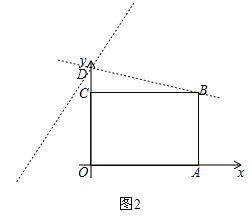
当过点![]() 时,代入可得
时,代入可得![]() ,解得
,解得![]()
![]() 直线
直线![]() :
:![]() 与矩形
与矩形![]() 没有公共点时
没有公共点时![]() 的取值范围为
的取值范围为![]()

练习册系列答案
相关题目