题目内容
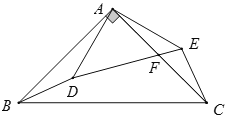
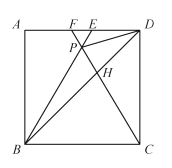
【题目】如图,在正方形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() 的延长线分别交
的延长线分别交![]() 于点
于点![]() ,连结
,连结![]() 与
与![]() 相交于点H.给出下列结论,
相交于点H.给出下列结论,
①△ABE≌△DCF;②△DPH是等腰三角形;③![]() ;④
;④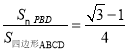 ,
,
其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
①利用等边三角形的性质以及正方形的性质得出∠ABE=∠DCF=30°,再直接利用全等三角形的判定方法得出答案;
②利用等边三角形的性质结合正方形的性质得出∠DHP=∠BHC=75°,进而得出答案;
③利用相似三角形的判定与性质结合锐角三角函数关系得出答案;
④根据三角形面积计算公式,结合图形得到△BPD的面积=△BCP的面积+△CDP面积-△BCD的面积,得出答案.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
在△ABE与△CDF中,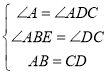 ,
,
∴△ABE≌△DCF,故①正确;
∵PC=BC=DC,∠PCD=30°,
∴∠CPD=75°,
∵∠DBC=45°,∠BCF=60°,
∴∠DHP=∠BHC=180![]() 75°,
75°,
∴PD=DH,
∴△DPH是等腰三角形,故②正确;
设PF=x,PC=y,则DC=AB=PC=y,
∵∠FCD=30°,
∴![]() 即
即![]() ,
,
整理得: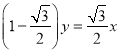
解得:![]() ,
,
则![]() ,故③正确;
,故③正确;
如图,过P作PM⊥CD,PN⊥BC,
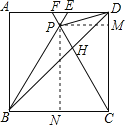
设正方形ABCD的边长是4,
∵△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°,
∴![]() ,
,
![]() ,
,
S△BPD=S四边形PBCD-S△BCD=S△PBC+S△PDC-S△BCD
![]()
![]()
![]()
![]() ,
,
∴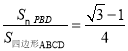 ,故④正确;
,故④正确;
故正确的有4个,
故选:A.

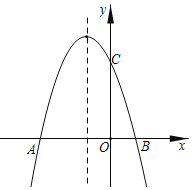
【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5