题目内容
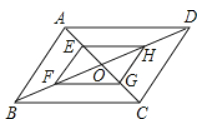
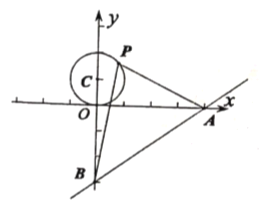
【题目】如图，已知直线
与
轴、
轴分别交于
，
两点，
是以
为圆心，1为半径的圆上一动点，连接
，
，当
的面积最大时，点的坐标为__________．
【答案】
【解析】
如图（见解析），过点P作
，过点C作
，延长EC交圆C于点F，过点F作
轴，连接AC，先根据直线与圆的关系求出当
的面积最大时，点P的位置，再利用直线的解析式、勾股定理求出OA、OB、AB的长，然后根据三角形相似的判定定理与性质即可得．
如图，过点P作，过点C作，延长EC交圆C于点F，过点F作轴，连接AC
则
要使的面积最大，则PD需最大
由直线与圆的关系得，当点P与点F重合时，PD取得最大值，最大值为
由题意得，
直线
，令
得
，则
令
得
，解得
，则
，解得
在
和
中，
，即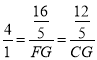
则点F的坐标为，即当的面积最大时，点P的坐标为
故答案为：．
练习册系列答案
相关题目
【题目】已知二次函数
的y与x的部分对应值如表：
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论：①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(
,2),B(
,3)是抛物线上两点,则
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
