题目内容
【题目】如图，抛物线y=ax2+bx+c与x轴交于点（-1，0），顶点坐标为（1，m），与y轴交点在（0，3），（0，4）之（不包含端点），现有下列结论：①3a+b＞0；②-
＜a＜-1；③关于x的方程ax2+bx+c=m-2有两个不相等的实数根：④若点M（-1.5，y1），N（2.5，y2）是函数图象上的两点，则y1=y2．其中正确结论的个数为（ ）
A.1B.2C.3D.4
【答案】A
【解析】
①根据抛物线的开口方向，可得a的取值范围；根据抛物线对称轴的公式，可建立起b与a的关系，即b=-2a，将其代入即可判断；
②根据与y轴交点范围，可得c的取值范围，将点（-1，0）代入抛物线公式，可得a与c的关系，进而得到a的取值范围；
③将方程ax2+bx+c=m-2转化为抛物线y=ax2+bx+c与直线
的交点的个数进行判断即可；
④根据自变量与对称轴的距离可以判断函数值的相对大小.
∵抛物线开口向下，
∴a＜0，
而抛物线的对称轴为直线x=
=1，即b=-2a，
∴3a+b=3a-2a=a＜0，所以①错误；
∵抛物线y=ax2+bx+c与x轴交于点（-1，0），
∴a-b+c=0，
∴3a+c=0，
∴c=-3a
∵2＜c＜3，
∴2＜-3a＜3，
∴-1＜a＜
，所以②错误；
∵抛物线的顶点坐标（1，m），m＞2，开口向下，与x轴有两个交点，
∴抛物线y=ax2+bx+c与直线y=m-2有两个交点，
∴关于x的方程ax2+bx+c=m-2有两个不相等的实数根，所以③正确；
∵抛物线的对称轴为直线x=1，而|-1.5-1|=2.5，|2.5-1|=1.5，
∴y1＜y2．所以④错误．
故选A．
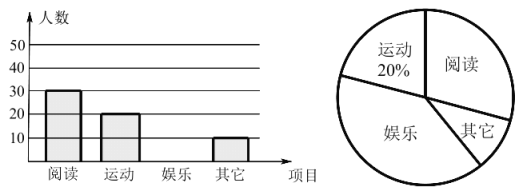
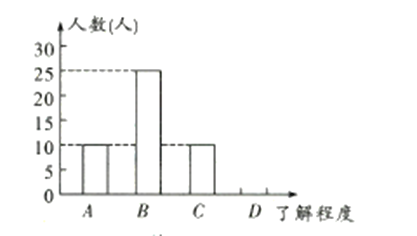
【题目】为响应市政府关于“垃圾不落地，市区更美丽”的主题宣传活动，某校随机调查了部分学生对垃圾分类知识的了解情况，对该校部分学生进行了问卷调查，并将调查结果分为
四类(其中
类表示“非常了解”，
类表示“比较了解”，
类表示“基本了解”，
类表示“不太了解”)．根据调查结果得到如下不完整的统计表和统计图．请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
，
．
补全条形统计图；
若该校共有学生
人，估计该校对垃圾分类知识“非常了解”的有多少人？
