题目内容
【题目】问题呈现:
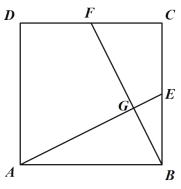
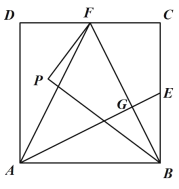
如图 1,在边长为 1 小的正方形网格中,连接格点 A、B 和 C、D,AB 和 CD 相交于点 P,求 tan ∠CPB 的值方法归纳:求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形,观察发现问题中∠ CPB不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 B、 E,可得 BE∥CD,则∠ABE=∠CPB,连接AE,那么∠CPB 就变换到 Rt△ABE 中.问题解决:
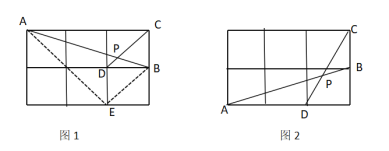
(1)直接写出图 1 中 tan CPB 的值为______;
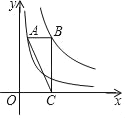
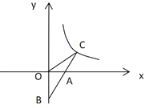
(2)如图 2,在边长为 1 的正方形网格中,AB 与 CD 相交于点 P,求 cos CPB 的值.
【答案】(1)2;(2)![]()
【解析】
(1)根据平行四边形的判定及平行线的性质得到∠CPB=∠ABE,利用勾股定理求出AE,BE,AB,证明△ABE是直角三角形,∠AEB=90°,即可求出tan CPB= tan ABE;
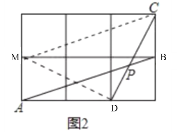
(2)如图2中,取格点D,连接CD,DM.通过平行四边形及平行线的性质得到∠CPB=∠MCD,利用勾股定理的逆定理证明△CDM是直角三角形,且∠CDM=90°,即可得到cos∠CPB=cos∠MCD.
解:(1)连接格点 B、 E,
∵BC∥DE,BC=DE,
∴四边形BCDE是平行四边形,
∴DC∥BE,
∴∠CPB=∠ABE,
∵AE=![]() ,BE=
,BE=![]() ,AB=
,AB=![]()
![]() ,
,
∴△ABE是直角三角形,∠AEB=90°,
∴tan∠CPB= tan∠ABE=![]() ,
,
故答案为:2;
(2)如图2所示,取格点M,连接CM,DM,
∵CB∥AM,CB=AM,
∴四边形ABCM是平行四边形,
∴CM∥AB,
∴∠CPB=∠MCD,
∵CM=![]() ,CD=
,CD=![]() ,MD=
,MD=![]() ,
,
![]() ,
,
∴△CDM是直角三角形,且∠CDM=90°,
∴cos∠CPB=cos∠MCD=![]() .
.

 备战中考寒假系列答案
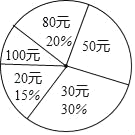
备战中考寒假系列答案【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.
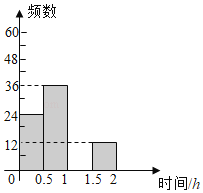
【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.