Question

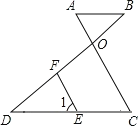
【题目】如图,AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A.

(1)求证：FE∥OC；

(2)若∠BOC比∠DFE大20，求∠OFE的度数.

Answer 1

【答案】（1）证明见解析（2）100°

【解析】分析：（1）由AB与CD平行，利用两直线平行内错角相等得到一对角相等，再由已知角相等，等量代换得到一对同位角相等，利用同位角相等两直线平行即可得证；

（2）由EF与OC平行，利用两直线平行同旁内角互补得到一对角互补，利用等角的补角相等得到∠BOC+∠DFE=180°，结合∠BOC+∠DFE=180°，求出∠OFE的度数即可．

详解：（1）∵AB∥DC，∴∠C=∠A．∵∠1=∠A，∴∠1=∠C，∴FE∥OC；

（2∵FE∥OC，∴∠FOC+∠OFE=180°．∵∠FOC+∠BOC=180°，∠DFE+∠OFE=180°，∴∠BOC+∠DFE=180°．∵∠BOC﹣∠DFE=20°，∴∠BOC+∠DFE=180°，解得：∠DFE=80°，∴∠OFE=100°．