题目内容
如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB的中点，且OE=a，则菱形ABCD的周长为
- A.16a
- B.12a
- C.8a
- D.4a
C
分析：根据已知可得菱形性质和直角三角形斜边上的中线等于斜边的一半可以求得菱形的边长即AB=2OE，从而不难求得其周长．
解答：因为菱形的对角线互相垂直平分，根据直角三角形斜边上的中线等于斜边的一半，可得AB=2a，则菱形ABCD的周长为8a．故选C．
点评：此题主要考查学生对菱形的性质及中位线的性质的理解及运用．
分析：根据已知可得菱形性质和直角三角形斜边上的中线等于斜边的一半可以求得菱形的边长即AB=2OE，从而不难求得其周长．
解答：因为菱形的对角线互相垂直平分，根据直角三角形斜边上的中线等于斜边的一半，可得AB=2a，则菱形ABCD的周长为8a．故选C．
点评：此题主要考查学生对菱形的性质及中位线的性质的理解及运用．
练习册系列答案
相关题目
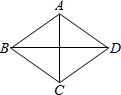如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（ ）| A、5 | B、10 | C、6 | D、8 |
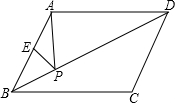
ME交射线CD于点N，连接MD、AN．
（2013•攀枝花）如图，在菱形ABCD中，DE⊥AB于点E，cosA=
如图，在菱形ABCD中，AE⊥BC，垂足为F，EC=1，∠B=30°，求菱形ABCD的周长．