题目内容
【题目】如图所示，位于
处的海上救援中心获悉：在其北偏东
方向的
处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东
相距
海里的
处救生船，并通知救生船，遇险船在它的正东方向处，现救生船沿着航线
前往处救援，若救生船的速度为海里/时，请问：
到
的最短距离是多少？
救生船到达处大约需要多长时间？（结果精确到
小时：参考数据：
，
，
，
，
，
）
【答案】（1）
到
的最短距离是33.51海里，（2）救生船到达B处大约需要1.7小时．
【解析】
（1）根据锐角三角函数可以求得CD和BD的长，从而可以解答本题；
（2）根据（1）中的结果可以解答本题．
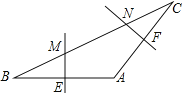
（1）过点C作CD⊥AB，垂足为D．
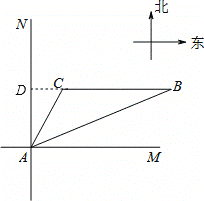
由题意知∠NAC＝30°，∠NAB＝68°，AC＝20，
∴∠CAB＝38°，∠BAM＝90°—68°＝22°，
∵BC∥AM，∴∠CBA＝∠BAM＝22°．
∵CD⊥AB，
∴∠ADC＝∠CDB＝90°．
在Rt△BCD中，sin∠CBD＝
，
∴CB＝
，
（2）救生船到达B处大约需要：t＝
＝1.7(小时)．
答：（1）到的最短距离是33.51海里，（2）救生船到达B处大约需要1.7小时.
练习册系列答案
开心蛙口算题卡系列答案
相关题目
