题目内容
【题目】阅读理解：对于二次三项式a2+2ab+b2，能直接用完全平方公式进行因式分解，得到结果为（a+b）2．而对于二次三项式a2+4ab﹣5b2，就不能直接用完全平方公式了，但我们可采用下述方法：
a2+4ab﹣5b2＝a2+4ab+4b2﹣4b2﹣5b2＝（a+2b）2﹣9b2，
＝（a+2b﹣3b）（a+2b+3b）＝（a﹣b）（a+5b）．
像这样把二次三项式分解因式的方法叫做添（拆）项法．
解决问趣：
（1）请利用上述方法将二次三项式a2+6ab+8b2分解因式；
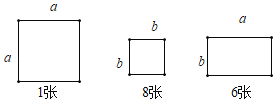
（2）如图，边长为a的正方形纸片1张，边长为b的正方形纸片8张，长为a，宽为b的长方形纸片6张，这些纸片可以拼成一个不重叠，无空隙的长方形图案，请画出示意图；
（3）已知x＞0，且x≠2，试比较分式
与
的大小．
【答案】（1）（a+2b）（a+4b）；（2）见解析；（3）
【解析】
（1）根据题目的引导，先分组，后运用公式法对原式进行因式分解；
（2）根据第一问的因式分解结果，对图形进行排列即可；
（3）对两个分式的分子和分母分别进行因式分解，然后对分式进行化简并比较大小.
解：（1）原式＝a2+6ab+9a2﹣b2＝（a+3b）2﹣b2＝（a+3b﹣b）（a+3b+b）＝（a+2b）（a+4b）；
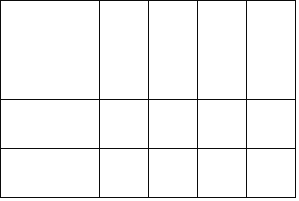
（2）如图：
（3）
；
；
∵x＞0，
∴x+4＜x+6，
∴.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
