题目内容
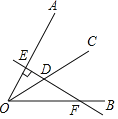
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=1,则DF=_____.
【答案】2
【解析】
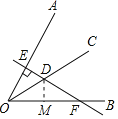
过点D作DM⊥OB,垂足为M,则DM=DE=1,在Rt△OEF中,利用三角形内角和定理可求出∠DFM=30°,在Rt△DMF中,由30°角所对的直角边等于斜边的一半可求出DF的长,此题得解.
解:过点D作DM⊥OB,垂足为M,如图所示.
∵OC是∠AOB的平分线,
∴DM=DE=1.
在Rt△OEF中,∠OEF=90°,∠EOF=60°,
∴∠OFE=30°,即∠DFM=30°.
在Rt△DMF中,∠DMF=90°,∠DFM=30°,
∴DF=2DM=2.
故答案为2

练习册系列答案
相关题目