题目内容
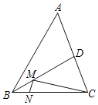
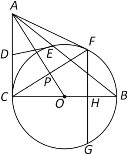
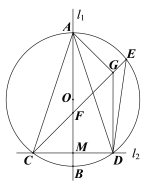
【题目】如图,直线l1⊥l2于点M,以l1上的点O为圆心画圆,交l1于点A,B,交l2于点C,D,OM=4,CD=6,点E为![]() 上的动点,CE交AB于点F,AG⊥CE于点G,连接DG,AC,AD.
上的动点,CE交AB于点F,AG⊥CE于点G,连接DG,AC,AD.
(1)求⊙O的半径长;
(2)若DG∥AB,求DG的长;
(3)连接DE,是否存在常数k,使![]() 成立?若存在,请求出k的值;若不存在,请说明理由;
成立?若存在,请求出k的值;若不存在,请说明理由;
(4)当点G在AD的右侧时,请直接写出△ADG面积的最大值.
【答案】(1)5;(2)3或6;(3)存在,![]() ;(4)9
;(4)9
【解析】
(1)直接利用勾股定理即可求解;
(2)证得FM是△CDG的中位线,再证得△CFM∽△AFG,设参数结合比例线段即可求解;
(3)在CG上截取CH=DE,利用SAS证得△ACH≌△ADE,推出AH=AE,再根据等腰三角形三线合一的性质可证得HG=EG,从而求得答案;
(4)取AC的中点P,当PG⊥AD时,△ADG面积最大;利用勾股定理求得AD =AC的长,证得Rt△CDN![]() Rt△ADM,求得CN的长,利用三角形中位线定理求得PK的长,利用直角三角形斜边中线的性质结合三角形面积即可求解.
Rt△ADM,求得CN的长,利用三角形中位线定理求得PK的长,利用直角三角形斜边中线的性质结合三角形面积即可求解.
(1) 连接OC,
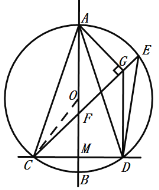
∵AM⊥CD,
∴CM=![]() CD,
CD,
∵CD=6,
∴CM=3
∵OM=4,
∴OC=![]() =
=![]() =5 ;
=5 ;
(2) ∵DG∥AB,且CM=MD,
∴CF=FG,
∴FM是△CDG的中位线,
∴DG=2FM,
∵∠CMF=∠AGF=90![]() ,
,
∠CFM=∠AFG,
∴△CFM∽△AFG,
∴![]() ,
,
∴![]() ,
,
设FM=![]() ,则AF=AM-FM=
,则AF=AM-FM=![]() ,
,
∴![]() ,
,
解得![]() 或3,
或3,
∴DG=3或6;
(3)存在常数k=2,理由如下:
在CG上截取CH=DE,连接AH,AE,
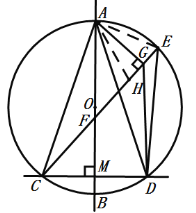
∵AB垂直平分CD,
∴AC=AD,
又∠ACH=∠ADE,
在△ACH和△ADE中,
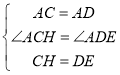 ,
,
∴△ACH≌△ADE (SAS) ,
∴AH=AE,
∵AG⊥HE,
∴HG=EG,
∴![]() ,
,
∴![]() ;
;
(4)取AC的中点P,当PG⊥AD时,△ADG面积最大;
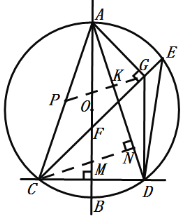
在Rt△AMC中,∠CMA=90![]() ,CM=3,AM=OA+OM=
,CM=3,AM=OA+OM=![]() ,
,
∴AD =AC=![]() ,
,
在Rt△AGC中,∠CGA=90![]() ,P为AC中点,
,P为AC中点,
∴PG =![]() AC
AC![]() ,
,
作CN⊥AD于N,
在Rt△CDN和Rt△ADM中,
∵∠CND=∠AMD=90![]() ,
,
∠CDN=∠ADM,
∴Rt△CDN![]() Rt△ADM,
Rt△ADM,
∴![]() ,
,
∴![]() ,
,
设PG交AD于K,
∵PK⊥AD,CN⊥AD,且P为AC中点,
∴PK是△ACN的中位线,
∴PK=![]() CN=
CN=![]() ,
,
∴GK=PG-PK=![]() ,
,
∴△ADG面积最大=![]() .
.