题目内容
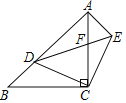
【题目】如图,已知在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点E,若D是AC的中点,连结DE.
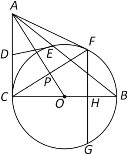
(1)求证:DE为⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)在(2)的条件下,过点A作⊙O的另一条切线,切点为F,过点F作FG⊥BC,垂足为H,且交⊙O于G点,连结AO 交CF于点P.求线段FG的长度.
【答案】(1)详见解析;(2)2;(3)![]() ;
;
【解析】
(1)连接OE、OD,易证OD是△ABC的中位线,利用中位线的性质可证明△COD≌△EOD, 所以∠DEO=∠DCO =90°,从而可知DE是⊙O的切线;
(2)由切线长定理得:DC=DE=![]() ,由点M是AC的中点可知AC=3,tan∠ABC=
,由点M是AC的中点可知AC=3,tan∠ABC=![]() ,所以BC=4,从而可知⊙O的半径为2;
,所以BC=4,从而可知⊙O的半径为2;
(3连结OF,由AC、AF都是⊙O的切线可知AO⊥CF,利用等面积可求得CF的长度,设OH为x,然后利用勾股定理可求得OH的长度,利用垂径定理即可求得FG.
(1)证明:连结OE、OD,
∵D是AC的中点,O是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AB,
∴∠COD=∠ABC,∠EOD=∠OEB,
又∵OB=OE,∴∠OEB=∠ABC,
∴∠COD=∠EOD,
在△COD与△EOD中,
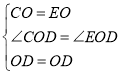
∴△COD≌△EOD(SAS),
∴∠DEO=∠DCO =90°,
∴DE是⊙O的切线.
(2)∵DC、DE分别是⊙O的切线,
∴![]() ,
,
∵D是AC的中点,
∴AC=2DC=3,
在Rt△ABC中,
∵![]() ,∴
,∴![]() ,
,
∴BC=4,
∴⊙O的半径为2.
(3)连结OF,
∵AC、AF都是⊙O的切线,
∴AC=AF,AO平分∠CAF,
∴AO⊥CF,且PC=PF,
∵AC=3,OC=2,
∴由勾股定理可得:![]() ,
,
由三角形面积法可得:![]() ACOC=
ACOC=![]() AOCP,
AOCP,
∴CP=![]() ,∴CF=
,∴CF=![]() ,
,
设OH=x,则CH=x+2,
由勾股定理可得:![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
在Rt△CFH中,
由勾股定理可得:![]() ,
,
∴由垂径定理可得:![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案