题目内容
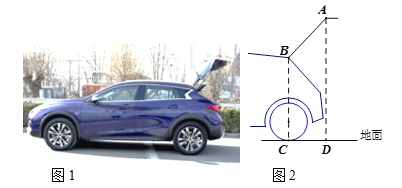
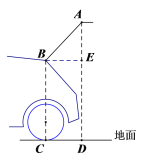
【题目】图1是某小型汽车的侧面示意图，图2表示该车的后备箱开起示意图，BC，AD都垂直于地面CD，∠ABC=138°，AB=80厘米，BC=130厘米．求点A到地面的距离（即AD的长，结果保留到1厘米）．参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11．
【答案】189厘米
【解析】
过点B作BE⊥AD于点E，由题意可知四边形BCDE为矩形，∠CBE=90°，DE=BC=130 cm，根据∠ABC=138°可得∠ABE=48°，利用sin∠ABE=
即可求得AE的长，进而可求得AD长即可
解：过点B作BE⊥AD于点E，
则四边形BCDE为矩形，∠CBE=90°，DE=BC=130 cm
因为∠ABC=138°
所以∠ABE=48°
因为在Rt△ABE中，sin∠ABE=
所以AE=AB×sin48°≈80×0.74=59.2
所以AD=130+59.2=189.2 cm≈189 cm
答：点 A 到地面的距离为189厘米
练习册系列答案
相关题目
【题目】甲、乙两超市(大型商场)同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满
元，均可得到一次摸奖的机会．在一个纸盒里装有
个红球和个白球（编号分别为红1、红、白1、白），除颜色外其它都相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券（在他们超市使用时，与人民币等值）的多少（如表）
甲超市：
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
乙超市：
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
（1）列举出一次摸奖时两球的所有情况；
（2）如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由．
