��Ŀ����
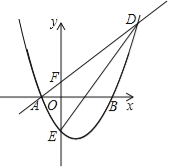
����Ŀ����ͼ,ֱ��AB��������ֱ��ڵ�A����B,��OA��OB�ij��ֱ�Ϊ����x2��6x+8=0����������OA��OB��,��C��y����,��OA�UAC=2�U5,ֱ��CD��ֱ��ֱ��AB�ڵ�P,��x���ڵ�D.
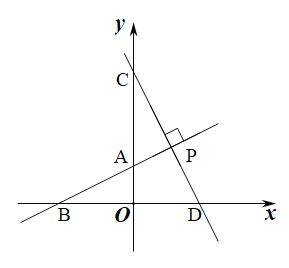
��1�������A����B������.
��2�������ֱ��CD�Ľ���ʽ.
��3������MΪ����ƽ��������һ��,������ƽ�����Ƿ���������ĵ�M,ʹ�Ե�B��P��D��MΪ������ı�����ƽ���ı���?������,��ֱ��д����M�����ꣻ��������,��˵������.
���𰸡���1��A(0,2)��B(��4,0);��2��ֱ��CD�Ľ���ʽ:yCD=��2x+7;��3�����ڣ�![]() ��
��![]() ��
��![]() ��
��
��������
��1������һԪ���η��̵Ľⷨ�ó�OA=2��OB=4�����ɵó���A��B�����ꣻ
��2���������ý�֮��Ĺ�ϵ�ó���BOA�ס�COD�����ɵó�D������꣬�����ô���ϵ������һ�κ�������ʽ��
��3�������P�����꣨2��3�����ٸ���ƽ���ı��ε����ʣ���PM=BD��M���ڵ�һ����ڶ����ޣ��Լ�BM=PDʱM�ڵ������ֱ����ֱ�ӵó��𰸣�
(1)��![]()
��![]()
��OA��OBΪ���̵�����������OA��OB
��OA=2��OB=4,
�� A(0,2)��B(��4,0),
(2)��OA:AC=2:5
�� AC=5
��OC=OA+AC=2+5=7
�� C(0,7),
�ߡ�BAO=��CAP,��CPB=��BOA=90O
���PBD=��OCD
�ߡ� BOA=��COD=90O
���BOA�ס�COD
��![]() =
=![]()
�� OD=![]() =
=![]() =
=![]() ,
,
��D(![]() ,0)
,0)
��ֱ��CD�Ľ���ʽΪ![]()
��x=0,y=7;x=![]() ,y=0�ֱ����ã�
,y=0�ֱ����ã�
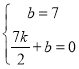
��![]()
��yCD=��2x+7,
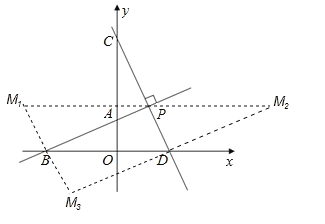
(3)���ڣ�
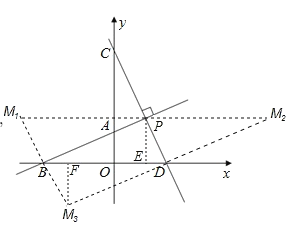
![]() ,
,![]()
![]() ��ֱ��AB�Ľ���ʽΪ��
��ֱ��AB�Ľ���ʽΪ��![]()
![]()
��ã�![]()
��ֱ��AB�Ľ���ʽΪ��![]()
��ֱ��AB��ֱ��CD����
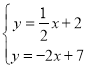
��ã�![]()
![]() P������
P������![]()
![]() ��
��![]()
![]()
��![]() ��ƽ���ı���
��ƽ���ı���
��![]()
![]()
![]()
��![]() ��ƽ���ı���
��ƽ���ı���
��![]()
![]()
![]()
P��![]() ��������
��������![]() ��
��![]() ����룬��
����룬��![]() ��������Ϊ-3
��������Ϊ-3
![]()
![]()
![]()
![]() �ĺ�����Ϊ2.5
�ĺ�����Ϊ2.5
![]()
![]() ������Ϊ
������Ϊ![]()
��������M���������![]() ��
��![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�