题目内容
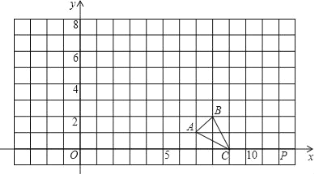
【题目】如图，A，B为反比例函数y＝
图象上的点，AD⊥x轴于点D，直线AB分别交x轴，y轴于点E，C，CO＝OE＝ED．
（1）求直线AB的函数解析式；
（2）F为点A关于原点的对称点，求△ABF的面积．
【答案】（1）y＝x﹣1（2）3
【解析】
（1）由已知线段相等，结合图形确定出三角形OCE与三角形ADE为全等的等腰直角三角形，设A（2a，a），代入反比例解析式求出a的值，确定出A与C坐标，利用待定系数法确定出直线AB解析式即可；
（2）由A坐标确定出F坐标，三角形ABF面积=三角形BCF面积+三角形OCF面积+三角形AOC面积，求出即可．
（1）∵CO＝OE＝ED，
∴△OCE和△ADE为全等的等腰直角三角形，
设A（2a，a），代入y＝
中，解得：a＝1或a＝﹣1（舍去），
∴点A（2，1），C（0，﹣1），
设直线AB解析式为y＝kx+b，
把A与C坐标代入得：
，
解得：
，
则直线AB的解析式为y＝x﹣1；
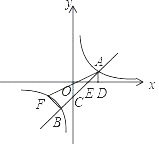
（2）∵点F为点A关于原点的对称点，
∴F（﹣2，﹣1），
联立得：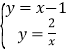
，
解得：
或
，即B（﹣1，﹣2），
如图，连接FC，作AG⊥y轴，BH⊥FC，由F，C的坐标可得FC∥x轴，
则S△ABF＝S△BFC+S△FCO+S△OCA＝
（CFBH+FCOC+OCAG）＝（2×1+2×1+1×2）＝3．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
