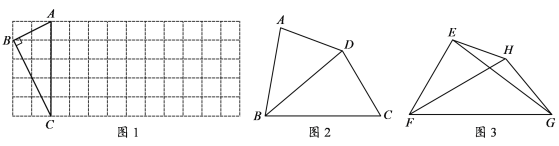
ЬтФПФкШн
ЁОЬтФПЁПХзЮяЯп![]() гы
гы![]() жсНЛгкAЃЌBСНЕуЃЌгы
жсНЛгкAЃЌBСНЕуЃЌгы![]() жсНЛгкЕуCЃЌСЌНгBCЃЎ
жсНЛгкЕуCЃЌСЌНгBCЃЎ
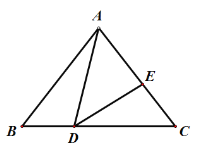
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжБЯпBCЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЪЧХзЮяЯпЩЯЮЛгкЕквЛЯѓЯоФкЕФвЛЕуЃЌСЌНгPCЃЌPBЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌвЛЖЏЕуQДгЕуPДгГіЗЂЃЌбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН
жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌАбХзЮяЯп![]() ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп
ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп![]() ЃЌдкаТХзЮяЯп
ЃЌдкаТХзЮяЯп![]() ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ
ЃЈ2ЃЉЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ![]() ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ
ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ, ЃЈ
ЃЉ, ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУГіНсТлЃЛ
ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШШЗЖЈГі![]() ЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГі
ЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГі![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШШЗЖЈГіЦНвЦКѓЕФХзЮяЯпНтЮіЪНЃЌНјЖјЧѓГі![]() ЃЌдкХаЖЯГі
ЃЌдкХаЖЯГі![]() НЈСЂЗНГЬМДПЩЕУГіНсТлЃЎ
НЈСЂЗНГЬМДПЩЕУГіНсТлЃЎ
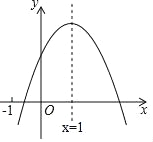
НтЃКЃЈ1ЃЉСю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ёр AЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ
ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
Сю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЎ
ЃЎ
ЁрC(0,3)ЃЎ
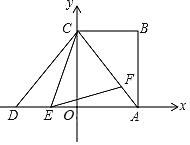
ЩшжБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌАбBЃЈ
ЃЌАбBЃЈ![]() ЃЌ0ЃЉДњШыЃЌЕУ
ЃЌ0ЃЉДњШыЃЌЕУ![]() ЃЎ
ЃЎ
НтЕУЃЌ![]() ЃЎ
ЃЎ
ЫљвджБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЙ§PзїPDЁЭ![]() жсНЛжБЯпBCгкMЃЎ
жсНЛжБЯпBCгкMЃЎ
Ёп жБЯпBCБэДяЪНЮЊ ![]() ЃЌ
ЃЌ
ЩшЕуMЕФзјБъЮЊ![]() ЃЌдђЕуP ЕФзјБъЮЊ
ЃЌдђЕуP ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
дђ![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрДЫЪБЃЌЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
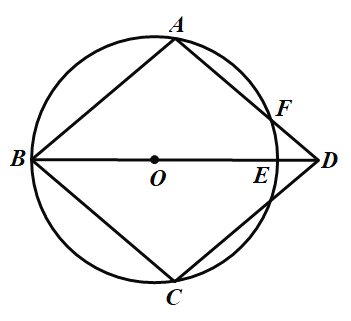
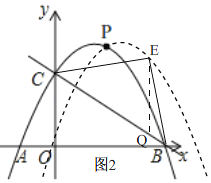
ИљОнЬтвтЃЌвЊЧѓЕФЯпЖЮPG+GH+HFЕФзюаЁжЕЃЌжЛашвЊАбетШ§ЬѕЯпЖЮЁААсЁБдквЛжБЯпЩЯЃЎШчЭМ1ЃЌзїЕуPЙигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌзїЕуFЙигк
ЃЌзїЕуFЙигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕуG,НЛ
жсгкЕуG,НЛ![]() жсгкЕуHЃЎИљОнжсЖдГЦадПЩЕУ
жсгкЕуHЃЎИљОнжсЖдГЦадПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ДЫЪБPG+GH+HFЕФзюаЁжЕ=![]() ЃЎ
ЃЎ

Ёп ЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁр Еу
ЃЉЃЌЁр Еу![]() ЕФзјБъЮЊЃЈ
ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёп ЕуFЪЧЯпЖЮBCЕФжаЕуЃЌ
Ёр ЕуFЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёр Еу![]() ЕФзјБъЮЊЃЈ
ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёп Еу![]() ЃЌPСНЕуЕФКсзјЯрЭЌЃЌЁр
ЃЌPСНЕуЕФКсзјЯрЭЌЃЌЁр![]() ЁЭ
ЁЭ![]() жсЃЎ
жсЃЎ
Ёп ![]() ЃЌPСНЕуЙигк
ЃЌPСНЕуЙигк![]() жсЖдГЦЃЌЁр
жсЖдГЦЃЌЁр![]() ЁЭ
ЁЭ![]() жсЃЎ
жсЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр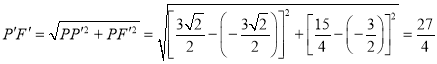 ЃЎ
ЃЎ
МДЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌдкХзЮяЯп![]() жаЃЌ
жаЃЌ
Сю![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
гЩЦНвЦжЊЃЌХзЮяЯп![]() ЯђгвЦНвЦЕН
ЯђгвЦНвЦЕН![]() ЃЌдђЦНвЦСЫ
ЃЌдђЦНвЦСЫ![]() ИіЕЅЮЛЃЌ
ИіЕЅЮЛЃЌ![]() ЃЌ
ЃЌ
ЩшЕу![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() гк
гк![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЃЌ
ЕФУцЛ§ЃЌ
![]() ЃЌ
ЃЌ
гЩЃЈ2ЃЉжЊЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЈЩс
ЃЈЩс![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ, ЃЈ
ЃЉ, ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ