Question

【题目】如图，在上依次有三点，的延长线交于过点作交的延长线于连交于点．

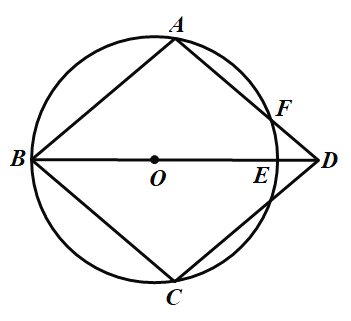
（1）求证：四边形是菱形；

（2）连接

当 时，点为弧的中点；

若且，则的半径是 ．

Answer 1

【答案】（1）见解析；（2）①72°，②3

【解析】

（1） 先由一组对边平行且相等可得四边形ABCD是平行四边形，再结合AB=BC证明是菱形；

（2）由点为弧的中点推出∠AOF=∠EOF= m，设参数表示△OFA各个角，根据三角形内角和列方程计算即可；

由设参数证明△AOF是等边三角形即可．

（1）证明：∵，

∴∠CBD＝∠ABD，

∵CD∥AB，

∴∠ABD＝∠CDB，

∴∠CBD＝∠CDB，

∴CB＝CD，

∵BE是⊙O的直径，

∴，

∴AB＝BC＝CD，

∵CD∥AB，

∴四边形ABCD是菱形；

（2）①F为弧AE的中点，设∠AOF=∠EOF= m

∴∠ABE=∠ADE=m

∴∠OAF=∠OFA=2m

∵∠AOF+∠OAF+∠OFA=180°

∴2m+2m+m=180°

∴m=36°

∴∠ABE=72°

②∵∠AOF＝3∠FOE，

设∠FOE＝x，则∠AOF＝3x，

∠AOD＝∠FOE+∠AOF＝4x，

∵OA＝OF，

∴∠OAF＝∠OFA＝（180﹣3x）°，

∵OA＝OB，

∴∠OAB＝∠OBA＝2x，

∴∠ABC＝4x，

∵BC∥AD，

∴∠ABC+∠BAD＝180°，

∴4x+2x+（180﹣3x）＝180，

x＝20°，

∴∠AOF＝3x＝60°，

∵OA＝OF，

∴△AOF是等边三角形，

∴OF＝AF＝3，

图（1） 图（2）