Question

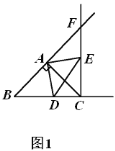
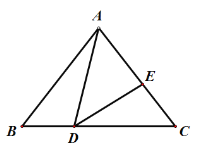
【题目】如图，△ABC中，AB=AC=6，BC=8，点D、E分别在BC，AC上，且∠ADE=∠B，若△ADE是等腰三角形，则BD的长为_________．

Answer 1

【答案】2或3.5

【解析】

根据等腰三角形的判定与性质，可得∠ADC与∠DAC的关系，根据三角形的外角的性质，可得∠AED=∠EDC+∠C=∠EDC+∠ADE，再根据等腰三角形的性质，可得答案．

∵AB=AC=6，
∴∠B=∠C=∠ADE．

当DA=DE时，

∴∠DAE=∠DEA，

∴∠AED=∠EDC+∠C=∠EDC+∠ADE，

∴∠DAC=∠ADC

∴DC=AC=6，

∴BD=2，
当AE=DE时，△ADE是等腰三角形，即∠DAE=∠ADE=∠B=∠C
∴△ADC∽△BAC，

∴，
∴，
∴，
∴；
综上所述：当BD=2或3.5时，△ADE是等腰三角形，
故答案为：2或3.5．