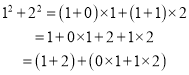��Ŀ����
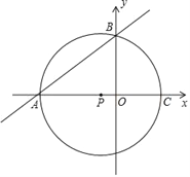
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᣬ
�ᣬ ![]() ��ֱ��ڵ�A��B��������
��ֱ��ڵ�A��B��������![]() ������A�͵�B����x�����һ������ΪC������D�ӵ�A��������ÿ��1����λ���ȵ��ٶ���O���˶���ͬʱ����E�ӵ�B��������ÿ��2����λ���ȵ��ٶ���A���˶������˶���ʱ��Ϊt�룬0��t��5.
������A�͵�B����x�����һ������ΪC������D�ӵ�A��������ÿ��1����λ���ȵ��ٶ���O���˶���ͬʱ����E�ӵ�B��������ÿ��2����λ���ȵ��ٶ���A���˶������˶���ʱ��Ϊt�룬0��t��5.
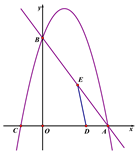
��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ����A��D��EΪ��������������AOB���ƣ�
��3������ADEΪ����������ʱ����t��ֵ��
��4�����������Ƿ����һ��F��ʹ����A��B��D��FΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д��F������ꣻ�������ڣ�˵������.
���𰸡���1�������ߵĽ���ʽΪ![]() ��
��
��2��t��ֵΪ![]() ��
��![]() ��
��
��3��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��
��4�����������ĵ�F���ڣ���������![]() ��4��8����
��4��8����![]() ��-8��.
��-8��.
����������1����B��C��������꣬���ô���ϵ��������������ߵĽ���ʽ����2�����á�ADE�ס�AOB�͡�AED�ס�AOB�������t��ֵ����3����E��EH��x���ڵ�H����D��DM��AB�ڵ�M�������t��ֵ����4���ֵ�ADΪ��ʱ����ADΪ�Խ���ʱ���������ĵ�F������.
�⣺(1)A��6,0����B��0,8����������֪![]() �����
����� ��
��
��![]() .
.
(2)�� A��6,0����B��0,8������OA=6��OB=8��AB=10����AD=t��AE=10-2t��
�ٵ���ADE�ס�AOBʱ�� ![]() ����
����![]() ����
����![]() ��
��
�ڵ���AED�ס�AOBʱ�� ![]() ����
����![]() ����
����![]() ��
��
����������t��ֵΪ![]() ��
��![]() .
.
(3) �ٵ�AD=AEʱ��t=10-2t����![]() ��
��
�ڵ�AE=DEʱ����E��EH��x���ڵ�H����AD=2AH���ɡ�AEH�ס�ABO�ã�AH=![]() ����
����![]() ����
����![]() ��
��
�۵�AD=DEʱ����D��DM��AB�ڵ�M����AE=2AM���ɡ�AMD�ס�AOB�ã�AM=![]() ����
����![]() ����
����![]() ��
��
����������t��ֵΪ![]() ��
��![]() ��
��![]() .
.
(4) �ٵ�ADΪ��ʱ����BF��x�ᣬ��![]() �����x=4����F��4��8����
�����x=4����F��4��8����
�ڵ�ADΪ�Խ���ʱ����![]() ����
����![]() �����
�����![]() ����x��0����
����x��0����![]() ����
����![]() .
.
�������������������ĵ�F���ڣ���������![]() ��4��8����
��4��8����![]() ��-8��.
��-8��.
���㾦�����⿼����κ����ۺ��⡢���������ε�֪ʶ������Ĺؼ���ѧ�����ϵ����ȷ����������ʽ��ѧ��������ۣ��÷��̵�˼�������⣬�����п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�