题目内容
【题目】在矩形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是
是 ![]() 边上一点,过点
边上一点,过点 ![]() 作
作 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() .
.
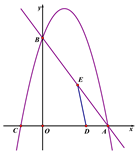
(1)如图1,若 ![]() ,则
,则 ![]() 度;
度;
(2)当以 ![]() ,
, ![]() ,
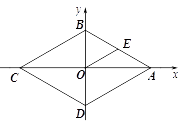
, ![]() 为顶点的三角形是等边三角形时,依题意在图2中补全图形并求
为顶点的三角形是等边三角形时,依题意在图2中补全图形并求 ![]() 的长;
的长;
(3)过点 ![]() 作
作 ![]() ∥
∥ ![]() 交射线
交射线 ![]() 于点
于点 ![]() ,请探究:当
,请探究:当 ![]() 为何值时,以
为何值时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
【答案】
(1)90
(2)
解:补全图形,如图所示.
∵四边形ABCD是矩形,
∴BC=AD=12,∠D=90°.
∵△ ![]() 是等边三角形,
是等边三角形,
∴GC=FC , ![]() .
.
∵∠2=∠3,
∴∠3=60°
在Rt△CDF中,DC=8 ,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
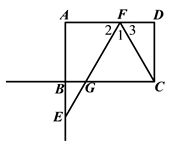
(3)
解:解法一:
过点F作FK⊥BC于点K,如图.
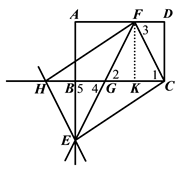
∵四边形ABCD是矩形,
∴∠5=∠ABC=90°,AD//BC.
∴∠1=∠3,∠2=∠AFG.
∵∠3=∠AFG,
∴∠1=∠2.
∴FG=FC.
∴GK=CK.
∵四边形FHEC是平行四边形,
∴FG=EG.
∵∠2=∠4,∠FKG=∠5=90°,
∴△FGK≌△EGB.
∴ ![]() .
.
∴当 ![]() 时,以
时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
解法二:如图.
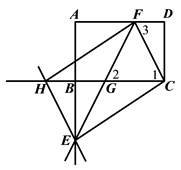
∵四边形ABCD是矩形,
∴∠ABG=90°,AD//BC.
∴∠1=∠3,∠2=∠AFG.
∵∠3=∠AFG,
∴∠1=∠2.
∴FG=FC.
∵四边形FHEC是平行四边形,
∴CG = HG ,FG=EG,HE=FC.
∴EG=EH.
又∵∠ABG=90°,
∴BG=BH=x.
∴CG=HG=2x.
∴x+2x=12.
∴x=4.
∴当 ![]() 时,以
时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
【解析】 (1)由矩形的性质得AD∥BC,∠D=90°,所以∠AFE=∠FGB,∠DFC=∠FCG,进而求得∠FGC=∠FCG,得到FC的长,再利用三角函数求得∠DFC=45°,即可得 ∠CFG=90°;
(2)先画出图形,由矩形与等边三角形的性质得到∠DFC=60°,利用三角函数求得FC的长,即为GC的长,再求BG即可;
(3)过点F作FK⊥BC于点K,由矩形的性质推出∠KCF=∠KGF,FG=FC,所以GK=CK.因为四边形FHEC是平行四边形,所以FG=EG.可得△FGK≌△EGB.所以BG=GK=KC= ![]() =4.
=4.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案