题目内容
【题目】
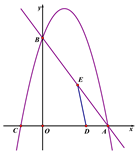
(1)如图①,∠AOB=60°,OD平分∠BOC,OE平分∠AOC,则∠EOD=度;
(2)若∠AOB=90°,其它条件不变,则∠EOD=;
(3)若∠AOB=α,其它条件不变,则∠EOD= .
(4)类比应用:如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为 , 并写出求解过程.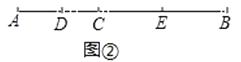
【答案】
(1)30°
(2)45°
(3)![]()
(4)DE= ![]() AB
AB
【解析】解:(1)∵OD平分∠BOC,OE平分∠AOC,∴∠DOC= ![]() ∠BOC,∠COE=
∠BOC,∠COE= ![]() ∠AOC,∴∠EOD=∠DOC+∠COE=
∠AOC,∴∠EOD=∠DOC+∠COE= ![]() ∠BOC+∠AOC=
∠BOC+∠AOC= ![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ![]() ∠AOB,∵∠AOB=60°,∴∠EOD=
∠AOB,∵∠AOB=60°,∴∠EOD= ![]() ×60°=30°;
×60°=30°;
⑵同理∠EOD= ![]() ∠AOB=
∠AOB= ![]() ×90°=45°;
×90°=45°;
⑶同理∠EOD= ![]() ∠AOB=
∠AOB= ![]() ;
;
⑷DE= ![]() AB.
AB.
理由如下:∵D是AC的中点,E是BC的中点,∴DC= ![]() AC,EC=
AC,EC= ![]() BC;∴DE=
BC;∴DE= ![]() AC+
AC+ ![]() BC=
BC= ![]() (AC+BC)=
(AC+BC)= ![]() AB.
AB.
(1)根据角平分线的定义得出∠DOC=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,再根据∠EOD=∠DOC+∠COE=
∠AOC,再根据∠EOD=∠DOC+∠COE=![]() ∠AOB,就可求出结果。
∠AOB,就可求出结果。
(2)根据角平分线的定义得出∠DOC=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,再根据∠EOD=∠DOC+∠COE=
∠AOC,再根据∠EOD=∠DOC+∠COE=![]() ∠AOB,就可求出结果。
∠AOB,就可求出结果。
(3)同理可得出∠EOD=![]() ∠AOB。
∠AOB。
(4)根据线段中点的定义,得出DC= ![]() AC,EC=
AC,EC= ![]() BC,再证明DE=
BC,再证明DE= ![]() AB即可。
AB即可。

练习册系列答案
相关题目