题目内容
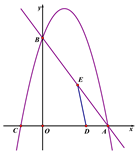
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.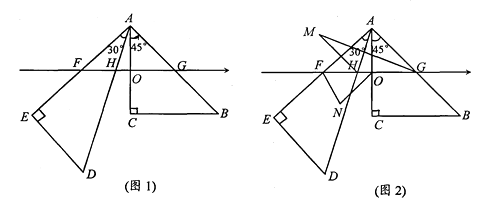
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 , 点H对应的数轴上的数是;
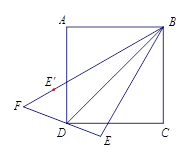
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
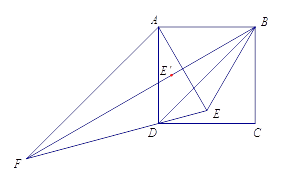
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.
【答案】
(1)-5;-1
(2)解:∵∠AHF的平分线和∠AGH的平分线交于点M,
∴2∠FHM=![]() ∠FHA,2∠HGM=
∠FHA,2∠HGM=![]() ∠HGA,
∠HGA,
∵∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,
∴2∠M+2∠HGM=∠HGA+∠HAG,
∴∠M=![]()
![]() ∠HAG=
∠HAG=![]()
![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]()
![]() ɑ+22.5
ɑ+22.5
(3)解: ∵∠EFH的平分线和∠FOC的平分线交于点N,
∴∠N=90°-![]()
![]() ∠FAO=90°-
∠FAO=90°-![]()
![]() ∠FAH-
∠FAH-![]()
![]() ∠OAH (可以直接利用∠N=90°-
∠OAH (可以直接利用∠N=90°-![]()
![]() ∠FAO)
∠FAO)
=90°-15°- ![]() ∠OAH
∠OAH
=75°- ![]() ∠OAH,
∠OAH,
∵∠M=![]()
![]() ∠OAH+22.5°,
∠OAH+22.5°,
∴∠M+∠N=97.5°.
【解析】解:(1)如图1,∵AC的中点过数轴的原点O,AC=8,
∴AO=4,
∵△AGH的面积是10,
∴![]() ×4×GH=10,
×4×GH=10,
解得GH=5,
又∵∠AOG=90,∠OAG=45,
∴OG=OA=4,
∴OH=1,
∴点H对应的数轴上的数是1,
∵△AHF的面积是8,
∴![]() FH4=8,
FH4=8,
解得FH=4,
∴OF=OH+FH=5,
∴点F对应的数轴上的数是5,
故答案为:5,1;
(1)根据中点的定义得出OA=4,根据三角形的面积得出![]() ×4×GH=10,从而得出GH的长度,根据等腰直角三角形的性质得出OG=OA=4,从而得出OH的长,得到点H对应的数轴上的数是1,再根据三角形的面积得出
×4×GH=10,从而得出GH的长度,根据等腰直角三角形的性质得出OG=OA=4,从而得出OH的长,得到点H对应的数轴上的数是1,再根据三角形的面积得出![]() FH4=8,从而得出FH的长,根据OF=OH+FH,得出OF的长,从而得出点F对应的数轴上的数是5;
FH4=8,从而得出FH的长,根据OF=OH+FH,得出OF的长,从而得出点F对应的数轴上的数是5;
(2)根据角平分线的定义得出2∠FHM= ∠FHA,2∠HGM= ∠HGA,根据三角形的外角定理得出∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,根据等量代换得出2∠M+2∠HGM=∠HGA+∠HAG,根据等式的性质从而得出答案∠M=![]() ∠HAG=
∠HAG=![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]() ɑ+22.5 ;
ɑ+22.5 ;
(3)直接利用结论∠N=90°-![]() ∠FAO=75°-
∠FAO=75°-![]() ∠OAH,又因∠M=
∠OAH,又因∠M=![]() ∠OAH+22.5°,从而得出∠M+∠N=97.5°.
∠OAH+22.5°,从而得出∠M+∠N=97.5°.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案