Question

【题目】已知二次函数的图象经过原点及点（， ），且图象与x轴的另一交点到原点的距离为1，求该二次函数解析式。

Answer 1

【答案】该二次函数解析式为y=﹣x2+x或y=x2+x．

【解析】试题分析：设二次函数的解析式为y=ax2+bx+c（a≠0），由图象与x轴的另一交点到原点的距离为1可得到抛物线与x轴的另一交点坐标为（1，0）或（-1，0），然后分别把（0，0）、（1，0）、（-，-）或（0，0）、（-1，0）、（-，-）代入解析式中得到两个方程组，解方程组即可确定解析式．

试题解析：设二次函数的解析式为y=ax2+bx+c（a≠0），

当图象与x轴的另一交点坐标为（1，0）时，

把（0，0）、（1，0）、（﹣，﹣）代入得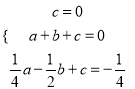，解方程组得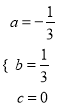，则二次函数的解析式为y=﹣x2+x；

当图象与x轴的另一交点坐标为（﹣1，0）时，把得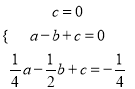，解方程组得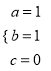，则二次函数的解析式为y=x2+x．

所以该二次函数解析式为y=﹣x2+x或y=x2+x．