��Ŀ����
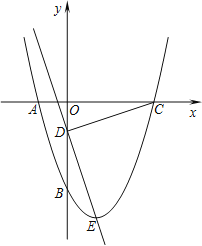
����Ŀ����ͼ�������߹�A��1��0����B����3��0����C��0����3�����㣬ֱ��AD���������ڵ�D����D�ĺ�����Ϊ��2����P��m��n�����߶�AD�ϵĶ��㣬����P��ֱ�ߴ�ֱ��x�ᣬ���������ڵ�Q��
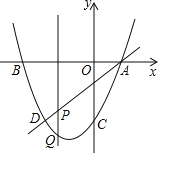
��1����ֱ��AD�������ߵĽ���ʽ��
��2�����߶�PQ�ij���l��m�Ĺ�ϵʽ��mΪ��ֵʱ��PQ���
��3����ƽ�����Ƿ�������㣨�ᡢ�����궼Ϊ������R��ʹ��P��Q��D��RΪ������ı�����ƽ���ı��Σ������ڣ������R�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��ֱ��AD�Ľ���ʽΪy��x��1�������ߵĽ���ʽΪ��y��x2+2x��3����2��l����m2��m+2 ����2��m��1������m����![]() ʱ��PQ������ֵΪ
ʱ��PQ������ֵΪ![]() ����3�����ڣ����������ĵ�R����6��������R1����2����2����R2����2����4����R3����2����1����R4����2����5����R5��0����3��R6��2����1����
����3�����ڣ����������ĵ�R����6��������R1����2����2����R2����2����4����R3����2����1����R4����2����5����R5��0����3��R6��2����1����
��������
��1��������y��ax2+bx��3��A��1��0����B����3��0����C��0����3�����������������ߵĽ���ʽ����D�����������Һ�����Ϊ��2�������D�����꣬����A��D�������꣬�ô���ϵ��������ֱ��AD�Ľ���ʽ��
��2����P��AD�ϣ���Q���������ϣ���������Ϊmʱ����Ӧ����������Ը��ݽ���ʽ��ʾ��������PQ�ij�l����P�㡢Q��������IJ���ǿ��Եõ�l��m�ĺ�����ϵʽ�������ݺ�������ֵ������mΪ��ֵʱ��PQ���PQ�����ֵҲ�������
��3��ʹP��Q��D��RΪ������ı�����ƽ���ı��Σ����Է����������һ��PQΪһ��ʱ����R����ֱ��x����2�ϣ��ٸ���PQΪ���ֵ���µ�����ֵ���õ�PQ������ֵ����ֱ��x����2�Ͽ����ҵ���R��λ�ã�ȷ����R�����꣬�ó��ڵ�D�Ϸ����ڣ��ڵ�D�·�Ҳ���ڣ�����PQΪһ���Խ���ʱ������ƽ���ı��ε����ʣ�PQ��DR����ƽ�֣���ʱR��C �غϣ�
�⣺��1���������ߵĽ���ʽΪy��ax2+bx+c����A��1��0����B����3��0��C��0����3������y��ax2+bx+c�ã�
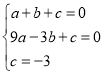 ��
��
��ã�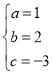 ��
��
�������ߵĽ���ʽΪ��y��x2+2x��3��
��x����2ʱ��y������2��2��4��3����3��
��D����2����3����
��ֱ��AD�Ľ���ʽΪy��kx+b����A��1��0����D����2����3������ã�
![]()
��ã�![]() ��
��
��ֱ��AD�Ľ���ʽΪy��x��1��
���ֱ��AD�Ľ���ʽΪy��x��1�������ߵĽ���ʽΪ��y��x2+2x��3��
��2���ߵ�P��ֱ��AD�ϣ�Q�������ϣ�P��m��n����
��n��m��1 Q��m��m2+2m��3��
��PQ�ij�l����m��1������m2+2m��3������m2��m+2 ����2��m��1��
�൱m����![]() ��
��![]() ʱ��PQ�ij�l�����������
ʱ��PQ�ij�l�����������![]() ��2������
��2������![]() ��+2��
��+2��![]() ��
��
���߶�PQ�ij���l��m�Ĺ�ϵʽΪ��l����m2��m+2 ����2��m��1��
��m����![]() ʱ��PQ������ֵΪ
ʱ��PQ������ֵΪ![]() ��
��
��3������PQΪƽ���ı��ε�һ�ߣ���Rһ����ֱ��x����2�ϣ���ͼ��
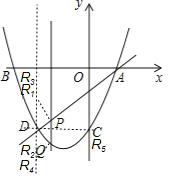
��PQ�ij�Ϊ0��PQ��![]() ��������
��������
��PQ��1��PQ��2��
��PQ��1ʱ����DR��1����ʱ���ڵ�D�Ϸ���R1����2����2�����ڵ�D�·���R2����2����4����
��PQ��2ʱ����DR��2����ʱ���ڵ�D�Ϸ���R3����2����1�����ڵ�D�·���R4����2����5����
����PQΪƽ���ı��ε�һ���Խ��ߣ���PQ��DR����ƽ�֣�
��PQ��1ʱ������x��1����x2+2x��3����1����ʱx����������
��PQ��2ʱ����x��1����x2+2x��3����2����ʱx1����1��x2��0����x1����1��R���C�غϣ���R5��0����3������x2��0����ʱR6��2����1��
�������������������ĵ�R�У�R1����2����2����R2����2����4����R3����2����1����R4����2����5����R5��0����3����
R6��2����1����
�𣺷��������ĵ�R����6��������R1����2����2����R2����2����4����R3����2����1����R4����2����5����R5��0����3��R6��2����1����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�