Question

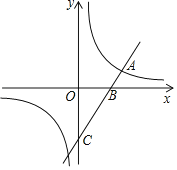
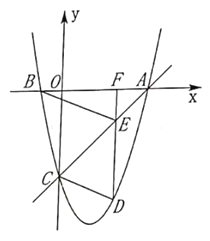
【题目】如图，已知点A（-6，0），B（2，0），点C在直线上，则使△ABC是直角三角形的点C的个数为（　　）

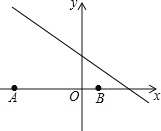
A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

根据∠A为直角，∠B为直角与∠C为直角三种情况进行分析．

如图，

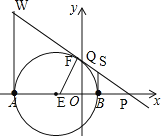
①当∠A为直角时，过点A作垂线与直线的交点W（-6，4），

②当∠B为直角时，过点B作垂线与直线的交点S（2，），

③若∠C为直角，

则点C在以线段AB为直径、AB中点E（-2，0）为圆心、4为半径的圆与直线的交点上．

在直线中，当x=0时y=2，即Q（0，2），

当y=0时x=6，即点P（6，0），

则PQ==4，

过AB中点E（-2，0），作EF⊥直线l于点F，

则∠EFP=∠QOP=90°，

∵∠EPF=∠QPO，

∴△EFP∽△QOP，

∴=，即=，

解得：EF=4，

∴以线段AB为直径、E（-2，0）为圆心的圆与直线恰好有一个交点．

所以直线上有一点C满足∠C=90°．

综上所述，使△ABC是直角三角形的点C的个数为3，

故选C．