题目内容
【题目】如图所示，某学校有一边长为20米的正方形
区域（四周阴影是四个全等的矩形，记为区域甲；中心区是正方形
，记为区域乙）．区域甲建设成休闲区，区域乙建成展示区，已知甲、乙两个区域的建设费用如下表：
区域 | 甲 | 乙 |
价格（百元米2） | 6 | 5 |
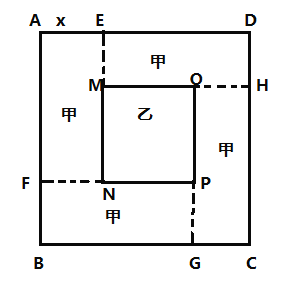
设矩形的较短边
的长为
米，正方形区域建设总费用为
百元．
（1）
的长为 米（用含的代数式表示）；
（2）求关于的函数解析式；
（3）当中心区的边长要求不低于8米且不超过12米时，预备建设资金220000元够用吗？请利用函数的增减性来说明理由．
【答案】（1）
；（2）y=
；（3）预备建设资金220000元不够用，见解析
【解析】
（1）根据矩形和正方形的性质解答即可；
（2）利用矩形的面积公式和正方形的面积公式解答即可；
（3）利用二次函数的性质和最值解答即可．
解：（1）设矩形的较短边
的长为
米，
，根据图形特点
．
（2）由题意知：
化简得：
（百元）
（3）由题知：
，解得
，
当x=4时，
，当x=6时，
，
将函数解析式变形：
，当时，y随x的增加而减少，所以
（百元），而
, 预备建设资金220000元不够用．
练习册系列答案
相关题目
