题目内容
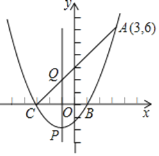
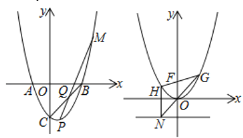
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,﹣2),顶点为P
(1)求抛物线的解析式;
(2)如图,若直线PM与BC交于Q,且sin∠CQP=![]() ,求点M的坐标;
,求点M的坐标;
(3)将抛物线平移至顶点为坐标原点,过F(0,![]() )的直线交抛物线于G、H,GO交直线y=﹣
)的直线交抛物线于G、H,GO交直线y=﹣![]() 于点N,求证:HN∥y轴.
于点N,求证:HN∥y轴.
【答案】(1)y=x2﹣x﹣2;(2)M(![]() ,
,![]() );(3)见解析
);(3)见解析
【解析】
(1)函数的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),即可求解;
(2)过点C作PM的平行线交x轴于点H,过点H作HG⊥BC于点G,求出点H(![]() ,0),确定直线PQ的表达式,即可求解.
,0),确定直线PQ的表达式,即可求解.
(3)直线HG的表达式为:y=x2x,则点N的坐标为(﹣![]() ,﹣
,﹣![]() ),由一元二次方程根与系数的关系得:x1x2=﹣
),由一元二次方程根与系数的关系得:x1x2=﹣![]() ,则x1=﹣
,则x1=﹣![]() ,即可求解.
,即可求解.
(1)函数的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
故﹣2a=﹣2,解得:a=1,
故函数的表达式为:y=x2﹣x﹣2;
(2)过点C作PM的平行线交x轴于点H,过点H作HG⊥BC于点G,
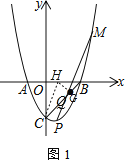
则∠HCB=∠CQP,
∵OB=OC=2,
∴∠OBC=45°,
设:OH=m,则BH=2﹣m,HG=BHsin∠OBC=![]() (2﹣m),HC=
(2﹣m),HC=![]() ,
,
sin∠HCB=![]() =sin∠CQP=
=sin∠CQP=![]() ,即:
,即: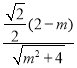 =
=![]() ,
,
解得:m=![]() (不合题意的值已舍去),则点H(
(不合题意的值已舍去),则点H(![]() ,0),
,0),
则直线CH表达式中的k值为:3,
设直线PQ的表达式为:y=3x+n,
将点(![]() ,﹣
,﹣![]() )的坐标代入上式并解得:
)的坐标代入上式并解得:
直线PM的表达式为:y=3x﹣![]() …②,
…②,
联立①②并解得:x=![]() 或
或![]() (舍去
(舍去![]() ),
),
故点M(![]() ,
,![]() );
);
(3)新函数的表达式为:y=x2…③,
设点H、G的坐标分别为(x1,x12)、(x2,x22),
则直线HG的表达式为:y=x2x,
则点N的坐标为(﹣![]() ,﹣
,﹣![]() );
);
设直线HG的表达式为:y=kx+![]() …④,
…④,
联立③④并整理得:x2﹣kx﹣![]() =0,
=0,
则x1x2=﹣![]() ,x1=﹣
,x1=﹣![]()
则点H的横坐标为:﹣![]() ,
,
点H、N的横坐标均为:﹣![]() ,
,
故HN∥y轴.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】如图所示,某学校有一边长为20米的正方形![]() 区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形
区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形![]() ,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
区域 | 甲 | 乙 |
价格(百元米2) | 6 | 5 |
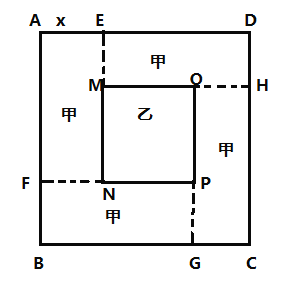
设矩形的较短边![]() 的长为
的长为![]() 米,正方形
米,正方形![]() 区域建设总费用为
区域建设总费用为![]() 百元.
百元.
(1)![]() 的长为 米(用含
的长为 米(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长要求不低于8米且不超过12米时,预备建设资金220000元够用吗?请利用函数的增减性来说明理由.