题目内容
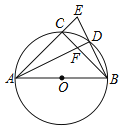
【题目】如图,AB是⊙O的直径,点C是弧AB的中点,D在⊙O上,延长AC、BD交于点E,AD与BC交于点F.若DF=2,DE=4,则CE的长为( )
A.2![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
【答案】C
【解析】
由“ASA”可证△ACF≌△BCE,可得CF=CE,AF=BE,通过证明△ADE∽△BDF,可得AD=2DB,AE=2BF,可求AC=BC=3CE,由勾股定理可求CE的长.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵点C是弧AB的中点,
∴AC=BC,
∵∠CAD=∠CBD,且∠ACF=∠ECB,且AC=BC,
∴△ACF≌△BCE(ASA)
∴CF=CE,AF=BE,
∵∠ADE=∠ADB,∠CBE=∠CAD,
∴△ADE∽△BDF
∴![]() ,
,
∴AD=2DB,AE=2BF,
∴AF+2=2(BE﹣DE)=2(AF﹣4)
∴AF=10=BE,
∵AE=2BF,
∴AC+CE=2(BC﹣CF)
∴AC=BC=3CE,
∵BC2+CE2=BE2,
∴10CE2=100,
∴CE=![]() ,
,
故选:C.

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(万元) |
甲 | 10 | a | 40 | 200 |
乙 | 18 | 8 | 40+0.05x2 | 100 |
其中a为常数,且5≤a≤8.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【题目】如图所示,某学校有一边长为20米的正方形![]() 区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形
区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形![]() ,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
区域 | 甲 | 乙 |
价格(百元米2) | 6 | 5 |
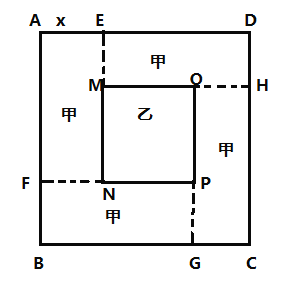
设矩形的较短边![]() 的长为
的长为![]() 米,正方形
米,正方形![]() 区域建设总费用为
区域建设总费用为![]() 百元.
百元.
(1)![]() 的长为 米(用含
的长为 米(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长要求不低于8米且不超过12米时,预备建设资金220000元够用吗?请利用函数的增减性来说明理由.